nbbp
nbbp.RmdWelcome to nbbp, an R package for inference of
parameters of negative binomial branching process models from final
outbreak size data. This vignette covers the basics of inferring
parameters from simple data, where every possible chain size is
observable and every observed chain size is known exactly. More advanced
forms of data are covered in the “Advanced data” vignette. Note that a
“chain” is not necessarily a linear structure and includes transmission
trees. That is, it consists of the first infected individual, any and
all individuals infected by the first, any and all individuals infected
by the second generation, and so forth. But as we are working with the
final size of a chain, each observation is simply an integer: the total
number of infections, including the first.
As our example, we will analyze Borealpox. Currently, there are seven
singleton cases which have been observed, each corresponding to a final
chain size of 1. The data is included in the package, though we could
have simply made it ourselves (e.g. rep(1, 7)).
## [1] 1 1 1 1 1 1 1Simple Bayesian inference
Fitting the model is accomplished by passing the data and the model
object to fit_nbbp_homogenous_bayes(), which internally
uses rstan for inference. This function allows significant
control over rstan settings, as well as adjustments to the
default priors (for more on those, see the vignette “Default priors”).
Here, for reproducibility, we will set the random seed, so that any time
we run this code (with the same version of rstan) we will
get the same answer.
fit <- fit_nbbp_homogenous_bayes(
all_outbreaks = borealpox,
seed = 42
)The output is a regular rstan::stanfit object, and can
be summarized in the usual ways. As we are performing Bayesian
inference, we should always check convergence diagnostics. (For more on
so doing, see the stan
manual, the rstan
reference, or Chapter 11.4 in
Bayesian Data Analysis.)
rstan::check_hmc_diagnostics(fit)##
## Divergences:## 0 of 10000 iterations ended with a divergence.##
## Tree depth:## 0 of 10000 iterations saturated the maximum tree depth of 10.##
## Energy:## E-BFMI indicated no pathological behavior.
rstan::summary(fit)$summary[, c("n_eff", "Rhat")]## n_eff Rhat
## r_eff 2258.851 1.000824
## inv_sqrt_dispersion 2614.954 1.001077
## dispersion 9478.288 1.000022
## exn_prob 3325.023 1.000598
## p_0 4546.211 1.000603
## lp__ 1852.968 1.002097Now that we can see our MCMC is trustworthy, we can look at what our
results are. There are 5 variables tracked in the object. Primarily, we
have
(r_eff) and
(dispersion). Additionally, we track two values which are
functions of
and
but can be useful in their own right. These are the probability that a
chain goes extinct (exn_prob) and the probability that any
one infection produces no additional infections (p_0). As
it is the native parameter of the model, we also have
(inv_sqrt_dispersion)
Let us see what we have estimated.
fit## Inference for Stan model: nbbp_homogenous.
## 4 chains, each with iter=5000; warmup=2500; thin=1;
## post-warmup draws per chain=2500, total post-warmup draws=10000.
##
## mean se_mean sd 2.5% 25% 50% 75% 97.5%
## r_eff 0.47 0.01 0.43 0.05 0.18 0.34 0.61 1.67
## inv_sqrt_dispersion 1.75 0.02 1.10 0.09 0.85 1.67 2.52 4.03
## dispersion 14966.82 14768.94 1437852.61 0.06 0.16 0.36 1.38 118.09
## exn_prob 0.99 0.00 0.03 0.89 1.00 1.00 1.00 1.00
## p_0 0.80 0.00 0.10 0.57 0.74 0.81 0.87 0.96
## lp__ -5.87 0.03 1.15 -8.91 -6.34 -5.53 -5.04 -4.71
## n_eff Rhat
## r_eff 2259 1
## inv_sqrt_dispersion 2615 1
## dispersion 9478 1
## exn_prob 3325 1
## p_0 4546 1
## lp__ 1853 1
##
## Samples were drawn using NUTS(diag_e) at Thu Jan 15 19:23:58 2026.
## For each parameter, n_eff is a crude measure of effective sample size,
## and Rhat is the potential scale reduction factor on split chains (at
## convergence, Rhat=1).We can see that the model is relatively confident , but there is still considerable uncertainty about its value. We can see even greater uncertainty about , which is typical in practice without a relatively large number of chains observed.
While rstan provides some basic plotting capabilities,
this is not the only way to do so. Here we extract and plot things
ourselves directly with ggplot, though we could also use the
bayesplot package which has many nice visualizations. Plots
show us
par_df <- rstan::extract(fit, pars = c("r_eff", "dispersion", "p_0", "exn_prob")) |>
as.data.frame()
par_df |>
ggplot(aes(x = r_eff, y = after_stat(density))) +
geom_histogram() +
theme_minimal() +
xlab("R")## `stat_bin()` using `bins = 30`. Pick better value `binwidth`.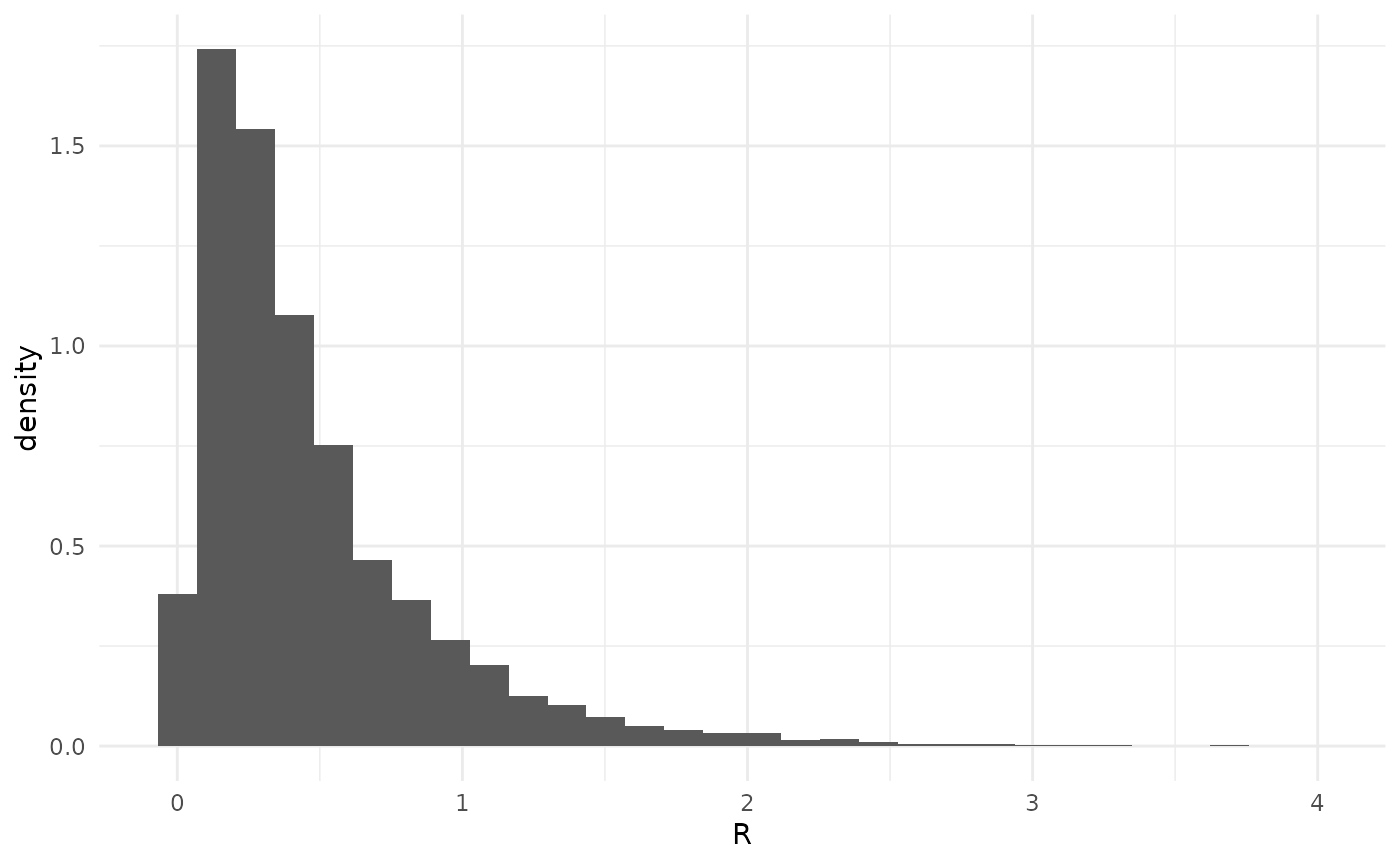 Here we can see that the posterior density is greatest for small values
of
,
as well as the long tails with larger values.
Here we can see that the posterior density is greatest for small values
of
,
as well as the long tails with larger values.
The uncertainty about the dispersion parameter often makes it more usefully considered on the log-scale.
par_df |>
ggplot(aes(x = log(dispersion), y = after_stat(density))) +
geom_histogram() +
theme_minimal() +
xlab("log(k)")## `stat_bin()` using `bins = 30`. Pick better value `binwidth`.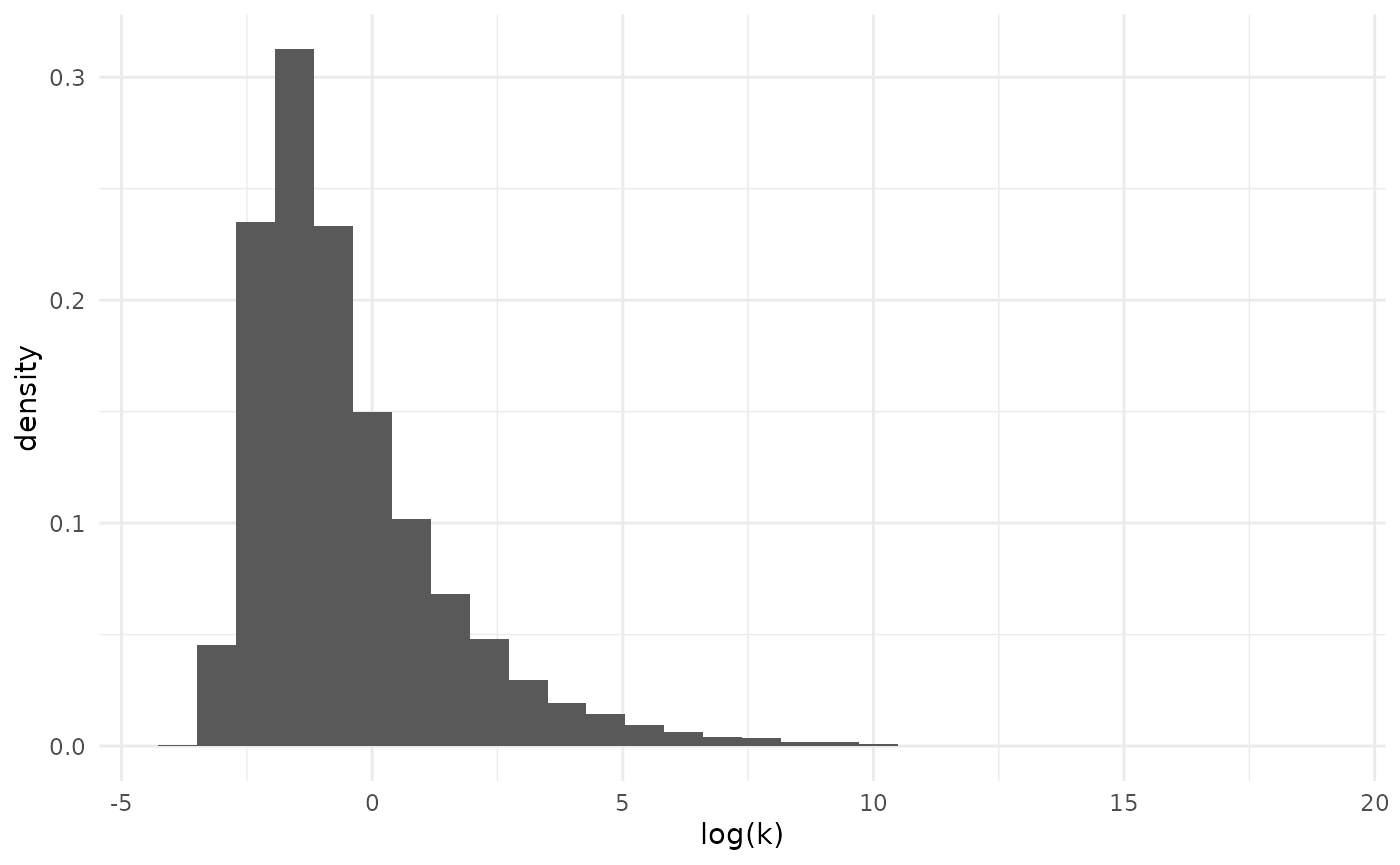 This shows us that, while there is considerable uncertainty, the model
favors relatively strong overdispersion.
This shows us that, while there is considerable uncertainty, the model
favors relatively strong overdispersion.
The probability that a chain goes extinct (exn_prob) is
a function of
and
.
par_df |>
ggplot(aes(x = exn_prob, y = after_stat(density))) +
geom_histogram() +
theme_minimal() +
xlab("extinction probability")## `stat_bin()` using `bins = 30`. Pick better value `binwidth`.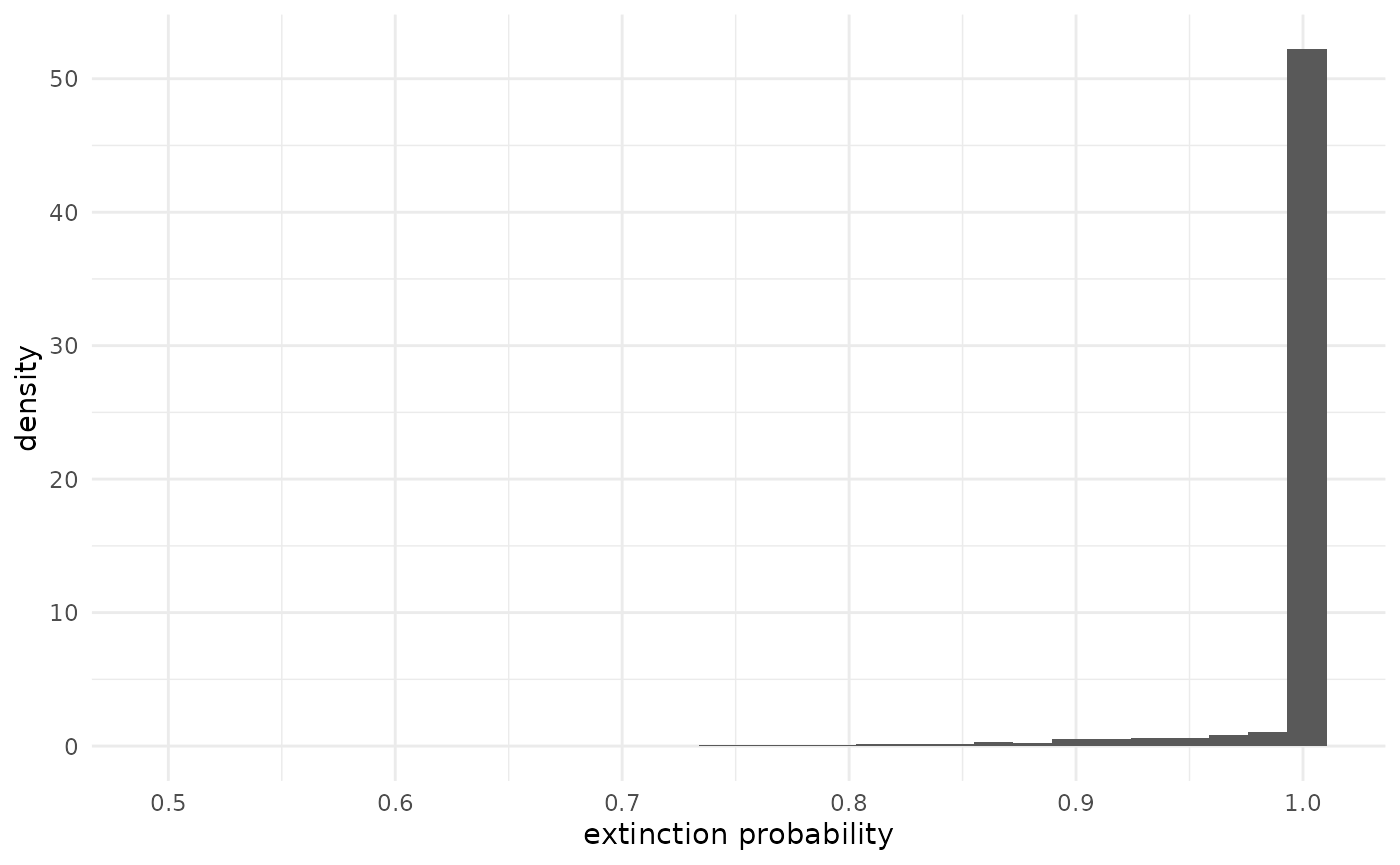 It is always 1 when
,
so since there is a 89% probability that
,
most of the prior mass is on 1 exactly. Most of the rest of the mass is
on values near 1, but we can see the considerably uncertainty about
and
manifest in the long left tail. While it isn’t probable that 7 chains
went extinct if the extinction probability is only, say, 0.8, it is not
impossible
().
It is always 1 when
,
so since there is a 89% probability that
,
most of the prior mass is on 1 exactly. Most of the rest of the mass is
on values near 1, but we can see the considerably uncertainty about
and
manifest in the long left tail. While it isn’t probable that 7 chains
went extinct if the extinction probability is only, say, 0.8, it is not
impossible
().
The probability of 0 offspring (p_0) is also a function
of
and
,
and measures the probability that any particular infection produces no
more infections.
par_df |>
ggplot(aes(x = p_0, y = after_stat(density))) +
geom_histogram() +
theme_minimal() +
xlab("probability of 0 offspring")## `stat_bin()` using `bins = 30`. Pick better value `binwidth`.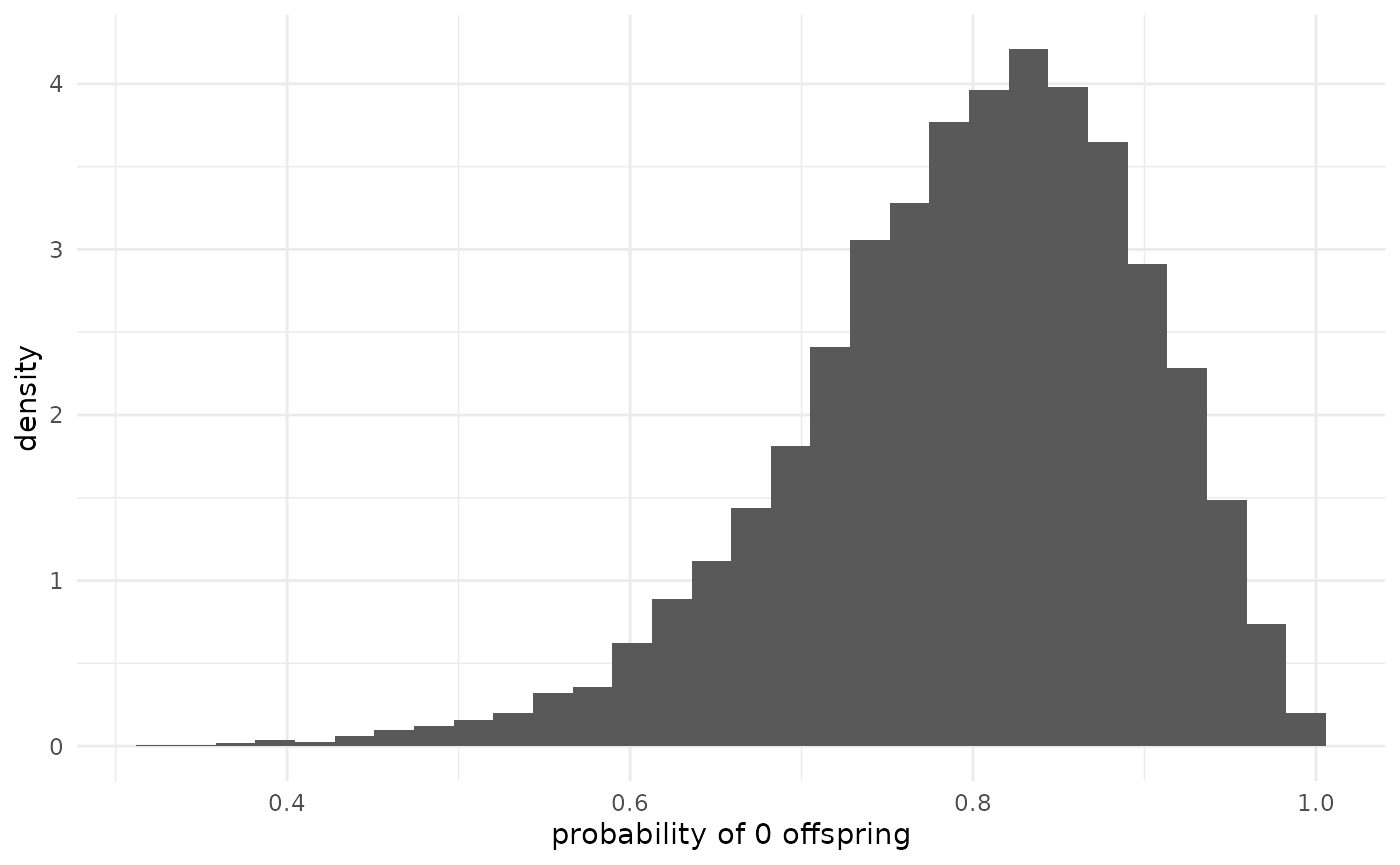 Since we have not seen any chains produce offspring, we should not be
surprised to see that this probability is near 1. (When there is strong
overdispersion (small
),
this can be near 1 even when
is above 1.) We might expect, since none of these cases have produced
any offspring, that the posterior would have a mode at 1. However, the
default priors pull towards regimes where this probability is smaller
(larger
and
both make it more likely that an infection has offspring), as can be
seen in the plot in the “Default priors” vignette.
Since we have not seen any chains produce offspring, we should not be
surprised to see that this probability is near 1. (When there is strong
overdispersion (small
),
this can be near 1 even when
is above 1.) We might expect, since none of these cases have produced
any offspring, that the posterior would have a mode at 1. However, the
default priors pull towards regimes where this probability is smaller
(larger
and
both make it more likely that an infection has offspring), as can be
seen in the plot in the “Default priors” vignette.
Simple maximum likelihood inference
The package also supports maximum likelihood inference. We do not
suggest using maximum likelihood as the primary form of inference, but
sometimes one may wish to see the results. This can be accomplished with
fit_nbbp_homogenous_ml() which has much the same interface
as fit_nbbp_homogenous_bayes(). By default, this attempts
to obtain 10 converged search replicates from random starting locations,
and will adaptively determine an appropriate method for producing
confidence intervals.
fit_ml <- fit_nbbp_homogenous_ml(
all_outbreaks = borealpox,
seed = 42,
ci_width = 0.95
)The object returned here is a slightly enriched version of what is
returned by rstan::optimizing for the replicate search
which produced the maximum maximized likelihood.
fit_ml## $par
## r_eff inv_sqrt_dispersion dispersion exn_prob
## 6.770924e+00 2.411232e+05 1.719975e-11 1.000000e+00
## p_0
## 1.000000e+00
##
## $value
## [1] -3.214485e-09
##
## $return_code
## [1] 0
##
## $theta_tilde
## r_eff inv_sqrt_dispersion dispersion exn_prob p_0
## [1,] 6.770924 241123.2 1.719975e-11 1 1
##
## $convergence
## min max
## log_likelihood -9.587682e-09 -3.214485e-09
## r_eff 7.471339e-10 5.889395e+01
## dispersion 1.609900e-11 1.352528e+05
##
## $ci
## 2.5% 97.5%
## r_eff 7.63948e-10 42.56584
## dispersion 1.45387e-11 73516.09755
##
## $ci_method
## [1] "hybrid(parametric_bootstrap)"Here, $par tells us our maximum likelihood estimates of
the parameters (and the additionally-tracked variables), and
$ci the confidence intervals (for only
and
).
Additionally, $convergence returns the range of values of
,
,
and the maximized likelihood across all search replicates. When there
are wide (relative to the value) ranges observed, this signals
trouble.
Sometimes, we can understand the nature of issues with maximum
likelihood inference by examining the likelihood surface. The function
compute_likelihood_surface() computes this at a grid and
enables visualization.
r_vec <- exp(seq(log(1e-4), log(2), length.out = 100))
k_vec <- exp(seq(log(0.01), log(9999), length.out = 100))
lnl_surface <- compute_likelihood_surface(
borealpox,
r_grid = r_vec,
k_grid = k_vec
)
lnl_surface |>
ggplot(aes(x = r, y = k, fill = log_dens)) +
theme_minimal() +
geom_tile() +
scale_x_continuous(trans = "log") +
scale_y_continuous(trans = "log") +
xlab("R") +
scale_fill_viridis_c(option = "magma")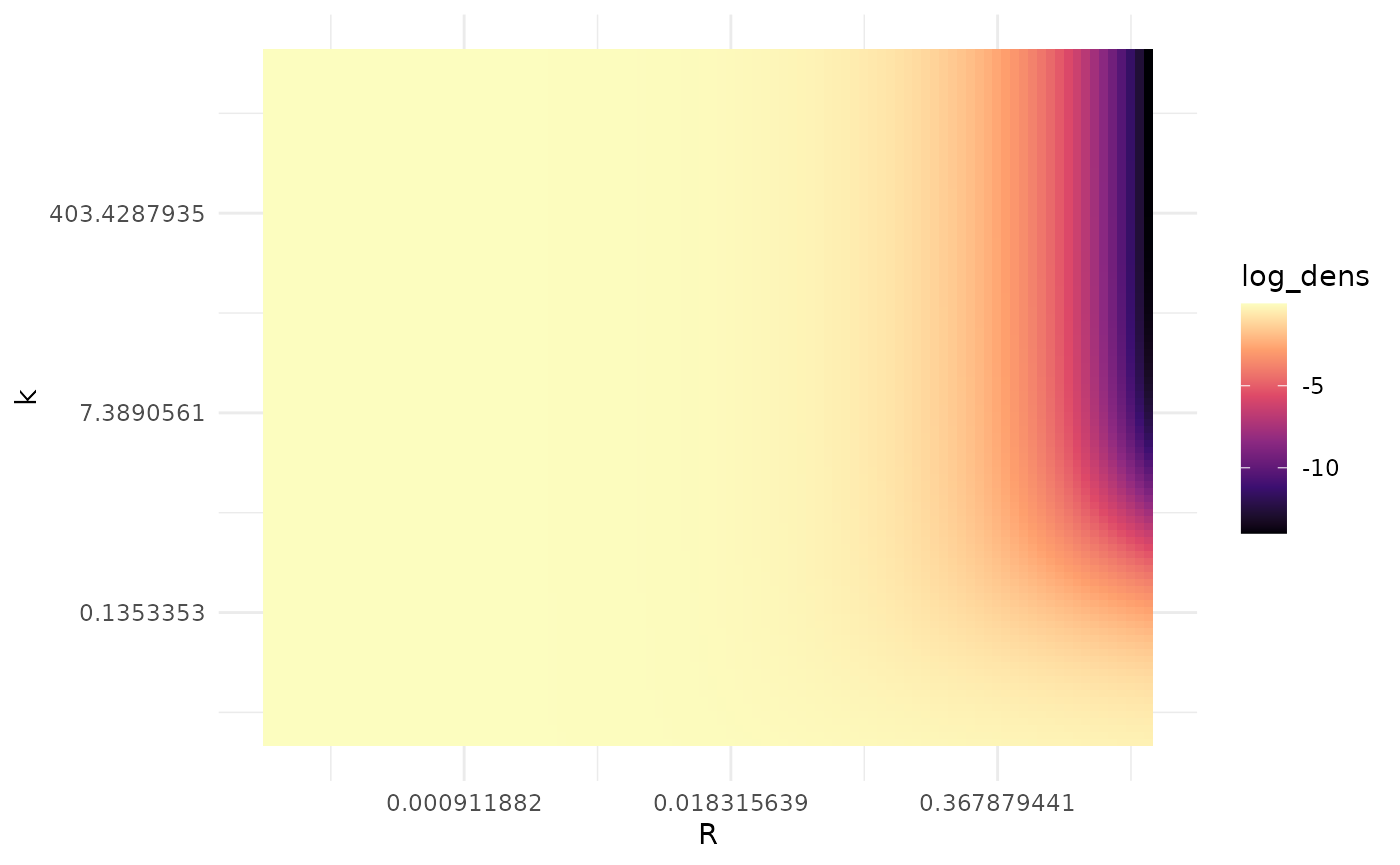
Roughly speaking, by Wilks’ theorem the region where the log-likelihood is within 12 units of the maximum value is within a bivariate 95% confidence region. We can see there is extensive uncertainty here, as most of this plot is within a 12 log-likelihood unit range of the maximum.
We also see that the the log-likelihood surface does not appear to have a single mode. It is easier to see what is going on if we focus in on where the likelihood is highest: small values of .
r_vec <- exp(seq(log(1e-4), log(0.02), length.out = 100))
lnl_surface <- compute_likelihood_surface(
borealpox,
r_grid = r_vec,
k_grid = k_vec
)
lnl_surface |>
ggplot(aes(x = r, y = k, fill = log_dens)) +
theme_minimal() +
geom_tile() +
scale_x_continuous(trans = "log") +
scale_y_continuous(trans = "log") +
xlab("R") +
scale_fill_viridis_c(option = "magma")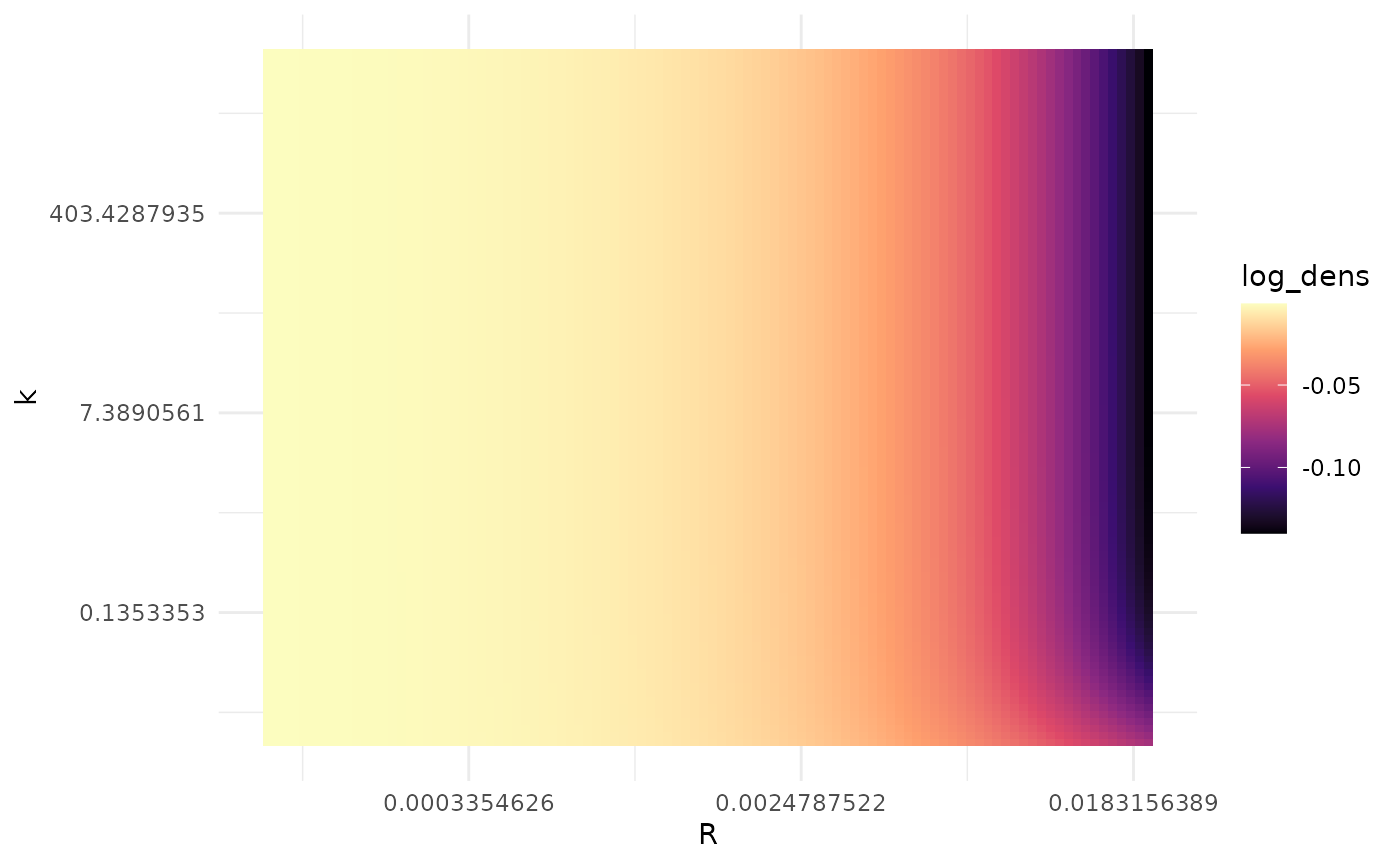
The likelihood increases as decreases, but once gets small, for a fixed the likelihood appears to be constant in . The presence of this ridge shape, rather than a single mode, likely explains the convergence difficulties we saw with maximum likelihood estimation. For sufficiently small , we can pick any and not change the likelihood, so the value of the optimizer ends up giving us is going to depend a lot on where it started.
“Is different?”
While inference in this package is focused on cases where is homogenous, we can still try to make comparisons about between scenarios.
Measles
For example, we might ask if is different in the two measles datasets included in the package. These correspond to cases in the United States from 1997-1999 and Canada from 1998-2001. To investigate this, we can simply fit the model, separately, to both datasets and examine the posteriors.
data(measles_us_97)
data(measles_canada_98)
us <- fit_nbbp_homogenous_bayes(measles_us_97, iter = 5000, seed = 42)
canada <- fit_nbbp_homogenous_bayes(measles_canada_98, iter = 5000, seed = 42)We have two sets of MCMC convergence diagnostics to check now.
rstan::check_hmc_diagnostics(us)##
## Divergences:## 0 of 10000 iterations ended with a divergence.##
## Tree depth:## 0 of 10000 iterations saturated the maximum tree depth of 10.##
## Energy:## E-BFMI indicated no pathological behavior.
rstan::summary(us)$summary[, c("n_eff", "Rhat")]## n_eff Rhat
## r_eff 5358.979 1.0005487
## inv_sqrt_dispersion 6294.843 0.9997029
## dispersion 4576.889 0.9999844
## exn_prob NaN NaN
## p_0 6285.057 0.9998974
## lp__ 4028.536 1.0011858We would normally be troubled by a NaN. However, when
the posterior probability that
is 1, the extinction probability is always 1. Convergence diagnostics
make use of the variance of a quantity in the posterior, and therefore
produce NaNs here.
rstan::check_hmc_diagnostics(canada)##
## Divergences:## 0 of 10000 iterations ended with a divergence.##
## Tree depth:## 0 of 10000 iterations saturated the maximum tree depth of 10.##
## Energy:## E-BFMI indicated no pathological behavior.
rstan::summary(canada)$summary[, c("n_eff", "Rhat")]## n_eff Rhat
## r_eff 4245.724 1.000902
## inv_sqrt_dispersion 4998.830 1.000269
## dispersion 2741.696 1.001163
## exn_prob 4062.019 1.001739
## p_0 4675.906 1.000146
## lp__ 3855.287 1.000061
r_df <- data.frame(
r = c(
unlist(rstan::extract(us, "r_eff")),
unlist(rstan::extract(canada, "r_eff"))
),
location = c(
rep("US", 10000),
rep("Canada", 10000)
)
)
r_df |>
ggplot(aes(x = r, fill = location, y = after_stat(density))) +
geom_histogram(position = "identity", alpha = 0.7) +
theme_minimal() +
xlab("R")## `stat_bin()` using `bins = 30`. Pick better value `binwidth`.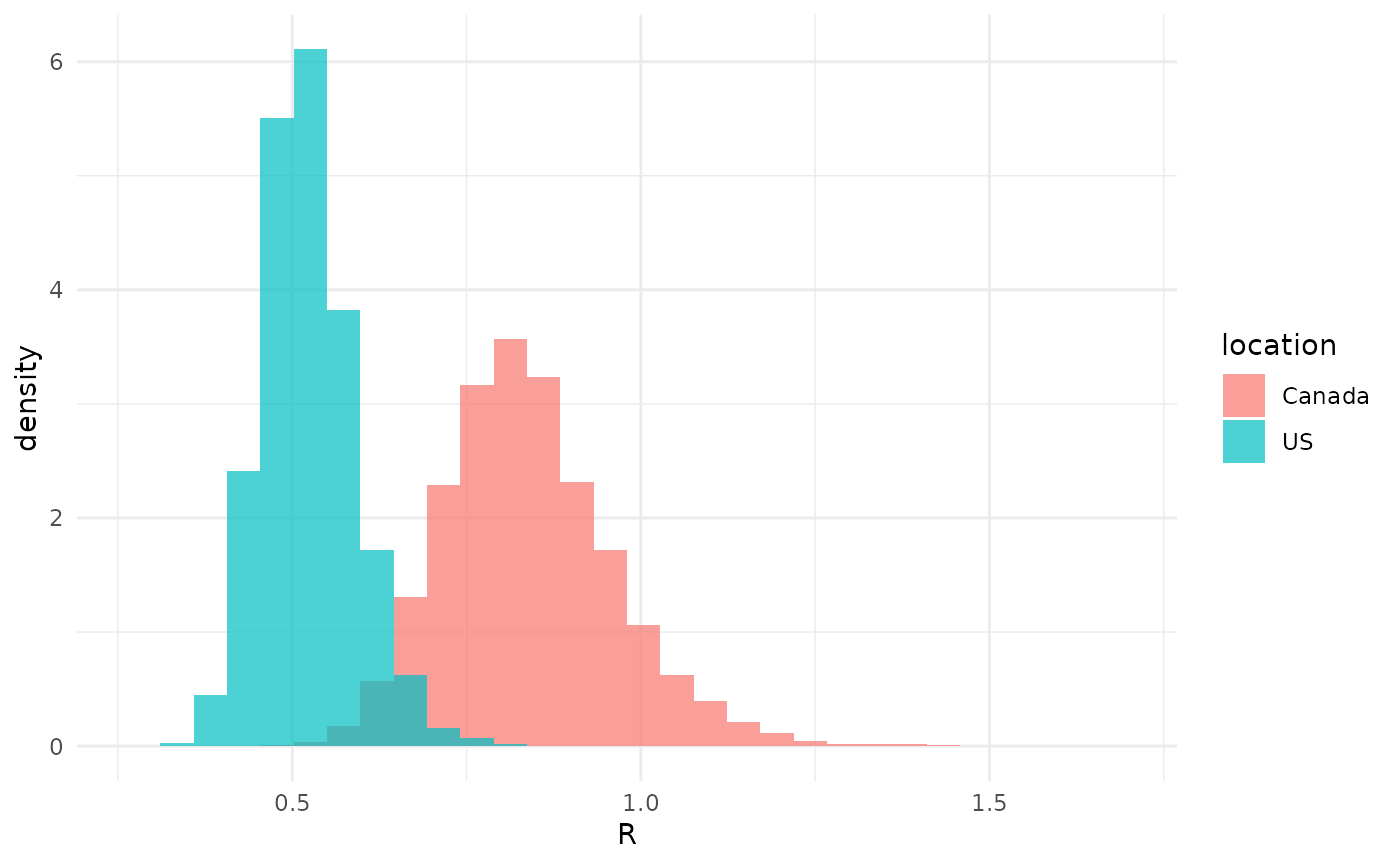 The posterior distributions on
exhibit rather low overlap, suggesting that
is in fact different.
The posterior distributions on
exhibit rather low overlap, suggesting that
is in fact different.
We can quantify this, if we like, by some measure of overlap of the posteriors. We might, for example, contemplate what percent of the posterior on is above the 2.5th percentile of the posterior on . We would then compute the 2.5th percentile of , find that it is 0.63, and count the percent of samples of which are larger than this and find that it is 6%. Or we could do this the other way around, and ask what percent of the posterior on is below below the 97.5th percentile of the posterior on . This is 5%.
These summaries are not entirely satisfying, as we have both an
arbitrary reference quantile and an asymmetric measure. We could instead
try to define, jointly, a single probability
and corresponding quantile
such that
.
That is, find the value of
for which the posterior probability that
is larger is equal to the posterior probability that
is smaller. Since
,
we can rearrange this equation and remove
,
simply writing
.
Once we solve for
,
we get our overlap percent
(%)
for free and can estimate it from our samples of either the posterior on
or on
.
This can’t simply be done in one chain of dplyr calls, so
we will need to write some code.
find_overlap <- function(r_small, r_large) {
# As pointed out, ECDFs are more efficient
# https://stats.stackexchange.com/questions/122857/how-to-determine-overlap-of-two-empirical-distribution-based-on-quantiles #nolint
p_r_small <- stats::ecdf(r_small)
p_r_large <- stats::ecdf(r_large)
loss_fn <- function(q) {
((p_r_small(q) + p_r_large(q)) - 1)^2
}
optimize(loss_fn, range(c(r_small, r_large)))$minimum
}
q <- find_overlap(
r_df |> dplyr::filter(location == "US") |> dplyr::pull(r),
r_df |> dplyr::filter(location == "Canada") |> dplyr::pull(r)
)
overlap <- 1.0 - mean(
r_df |>
dplyr::filter(location == "US") |>
dplyr::pull(r)
<= q
)This gives us an overlap of 4%.
MERS-CoV
As another example, we might ask if is different for MERS-CoV in the Arabian Peninsula after June 1, 2013 (compared to before). Again, we fit both datasets separately and compare.
data(mers_pre_june)
data(mers_post_june)
before <- fit_nbbp_homogenous_bayes(mers_pre_june, iter = 5000, seed = 42)
after <- fit_nbbp_homogenous_bayes(mers_post_june, iter = 5000, seed = 42)Again we have two sets of MCMC convergence diagnostics to check.
rstan::check_hmc_diagnostics(before)##
## Divergences:## 0 of 10000 iterations ended with a divergence.##
## Tree depth:## 0 of 10000 iterations saturated the maximum tree depth of 10.##
## Energy:## E-BFMI indicated no pathological behavior.
rstan::summary(before)$summary[, c("n_eff", "Rhat")]## n_eff Rhat
## r_eff 2961.937 1.000446
## inv_sqrt_dispersion 3475.358 1.000534
## dispersion 3149.092 1.000688
## exn_prob 2856.570 1.000584
## p_0 4900.390 1.000125
## lp__ 2261.079 1.001697
rstan::check_hmc_diagnostics(after)##
## Divergences:## 0 of 10000 iterations ended with a divergence.##
## Tree depth:## 0 of 10000 iterations saturated the maximum tree depth of 10.##
## Energy:## E-BFMI indicated no pathological behavior.
rstan::summary(after)$summary[, c("n_eff", "Rhat")]## n_eff Rhat
## r_eff 2271.476 1.000319
## inv_sqrt_dispersion 2587.110 1.000519
## dispersion 2345.970 1.001626
## exn_prob 2644.307 1.000898
## p_0 4597.428 1.000400
## lp__ 1385.952 1.000513
r_df <- data.frame(
r = c(
unlist(rstan::extract(before, "r_eff")),
unlist(rstan::extract(after, "r_eff"))
),
time = c(
rep("before", 10000),
rep("after", 10000)
)
)
r_df |>
ggplot(aes(x = r, fill = time, y = after_stat(density))) +
geom_histogram(position = "identity", alpha = 0.7) +
theme_minimal() +
xlab("R")## `stat_bin()` using `bins = 30`. Pick better value `binwidth`.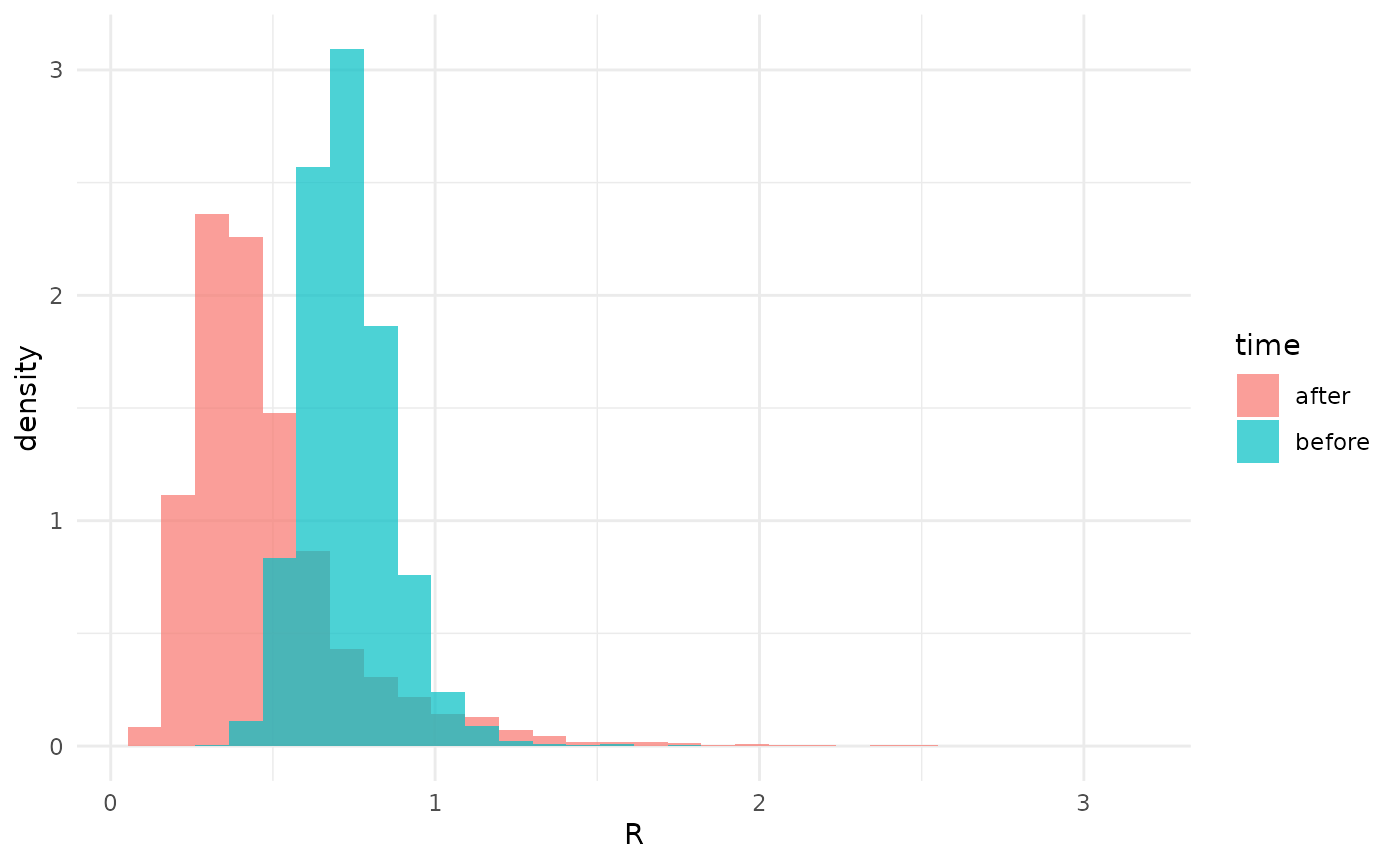 The posterior for the later cases completely covers the posterior for
the earlier ones. Clearly, there is no evidence for a difference in
.
The posterior for the later cases completely covers the posterior for
the earlier ones. Clearly, there is no evidence for a difference in
.