Observation processes for count data

This tutorial demonstrates how to use the Counts observation process to model count data such as hospital admissions, emergency department visits, or deaths.

Code

import jax.numpy as jnp
import numpy as np
import numpyro
import plotnine as p9
import pandas as pd
from pathlib import Path
import sys
import warnings
from plotnine.exceptions import PlotnineWarning

warnings.filterwarnings("ignore", category=PlotnineWarning)

import matplotlib.pyplot as plt

from pyrenew.observation import Counts, NegativeBinomialNoise, PoissonNoise
from pyrenew.deterministic import DeterministicVariable, DeterministicPMF
from pyrenew import datasets

Overview

Count observation processes model the lag between infections and an observed outcome such as hospital admissions, emergency department visits, confirmed cases, or deaths. Observed data can be aggregated or available as subpopulation-level counts, which are modeled by classes Counts and CountsBySubpop, respectively.

Count observation processes transform infections into predicted counts by applying an event probability and/or ascertainment rate and convolving with a delay distribution.

The predicted observations on day \(t\) are:

\[\lambda_t = \alpha \cdot \sum_{d=0}^{D} I_{t-d} \cdot p_d\]

where:

• \(I_{t-d}\) is the number of incident (new) infections on day \(t-d\) (i.e., \(d\) days before day \(t\))
• \(\alpha\) is the rate of ascertained counts per infection (e.g., infection-to-hospital admission rate). This can model a mix of biological effects (e.g. some percentage of infections lead to hospital admissions, but not all) and reporting effects (e.g. some percentage of admissions that occur are reported, but not all).
• \(p_d\) is the delay distribution from infection to observation, conditional on an infection leading to an observation
• \(D\) is the maximum delay

Discrete observations are generated by sampling from a noise distribution—e.g. Poisson or negative binomial—to model reporting variability. Poisson assumes variance equals the mean; negative binomial accommodates the overdispersion common in surveillance data.

Note on terminology: In real-world inference, incident infections are typically a latent (unobserved) quantity and must be estimated from observed data like hospital admissions. In this tutorial, we simulate the observation process by specifying infections directly and showing how they produce hospital admissions through convolution and sampling.

Hospital admissions example

For hospital admissions data, we construct a Counts observation process. The delay is the key mechanism: infections from \(d\) days ago (\(I_{t-d}\)) contribute to today’s hospital admissions (\(\lambda_t\)) weighted by the probability (\(p_d\)) that an infection leads to hospitalization after exactly \(d\) days. The convolution sums these contributions across all past days.

The process generates hospital admissions by sampling from a negative binomial distribution:

\[Y_t \sim \text{NegativeBinomial}(\mu = \lambda_t, \text{concentration} = \phi)\]

The concentration parameter \(\phi\) (sometimes called \(k\) or the dispersion parameter) controls overdispersion: as \(\phi \to \infty\), the distribution approaches Poisson; smaller values allow greater overdispersion.

We use the negative binomial distribution because real-world hospital admission counts exhibit overdispersion—the variance exceeds the mean. The Poisson distribution assumes variance equals the mean, which is too restrictive. The negative binomial adds an overdispersion term:

\[\text{Var}[Y_t] = \mu + \frac{\mu^2}{\phi}\]

In this example, we use fixed parameter values for illustration; in practice, these parameters would be estimated from data using weakly informative priors.

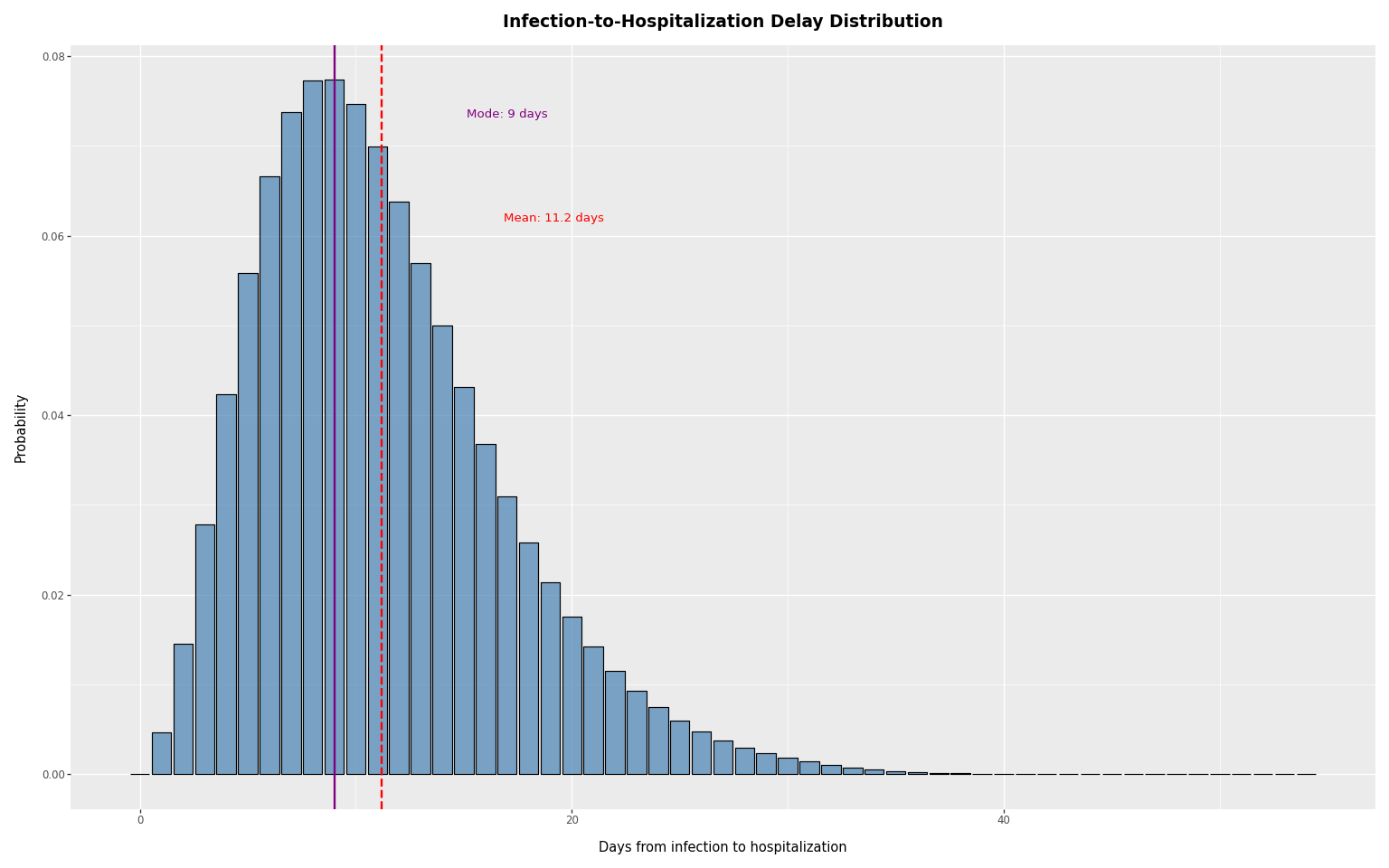
Infection-to-hospitalization delay distribution

The delay distribution specifies the probability that an infected person is hospitalized \(d\) days after infection, conditional on the infection leading to a hospitalization. For example, if hosp_delay_pmf[5] = 0.2, then 20% of infections that result in hospitalization will appear as hospital admissions 5 days after infection.

We load a delay distribution from PyRenew’s example datasets, compute summary statistics, and plot it. The distribution peaks around day 8-9 post-infection.

Code

inf_hosp_int = datasets.load_infection_admission_interval()
hosp_delay_pmf = jnp.array(inf_hosp_int["probability_mass"].to_numpy())
delay_rv = DeterministicPMF("inf_to_hosp_delay", hosp_delay_pmf)

# Summary statistics
days = np.arange(len(hosp_delay_pmf))
mean_delay = float(np.sum(days * hosp_delay_pmf))
mode_delay = int(np.argmax(hosp_delay_pmf))
sd = float(np.sqrt(np.sum(days**2 * hosp_delay_pmf) - mean_delay**2))
print(
    f"mode delay: {mode_delay},  mean delay: {mean_delay:.1f},  sd: {sd:.1f}"
)

mode delay: 9,  mean delay: 11.2,  sd: 5.7

Code

delay_df = pd.DataFrame(
    {"days": days, "probability": np.array(hosp_delay_pmf)}
)

plot_delay = (
    p9.ggplot(delay_df, p9.aes(x="days", y="probability"))
    + p9.geom_col(fill="steelblue", alpha=0.7, color="black")
    + p9.geom_vline(
        xintercept=mode_delay, color="purple", linetype="solid", size=1
    )
    + p9.geom_vline(
        xintercept=mean_delay, color="red", linetype="dashed", size=1
    )
    + p9.labs(
        x="Days from infection to hospitalization",
        y="Probability",
        title="Infection-to-Hospitalization Delay Distribution",
    )
    + p9.theme_grey()
    + p9.theme(plot_title=p9.element_text(size=14, weight="bold"))
    + p9.annotate(
        "text",
        x=mode_delay + 8,
        y=max(delay_df["probability"]) * 0.95,
        label=f"Mode: {mode_delay} days",
        color="purple",
        size=10,
    )
    + p9.annotate(
        "text",
        x=mean_delay + 8,
        y=max(delay_df["probability"]) * 0.8,
        label=f"Mean: {mean_delay:.1f} days",
        color="red",
        size=10,
    )
)
plot_delay

Creating a Counts observation process

A Counts object takes the following arguments:

• name: unique, meaningful identifier for this observation process (e.g., "hospital", "deaths")
• ascertainment_rate_rv: the probability an infection results in an observation (e.g., IHR)
• delay_distribution_rv: delay distribution from infection to observation (PMF)
• noise: noise model (PoissonNoise() or NegativeBinomialNoise(concentration_rv))

Observation processes are components in multi-signal models, where each signal must have a unique name. This name prefixes all numpyro sample sites (e.g., "hospital" creates sites "hospital_obs" and "hospital_predicted"), ensuring distinct identifiers in the inference trace.

For hospital admissions, the ascertainment rate is specifically called the infection-hospitalization rate (IHR). In this example, the percentage of infections which lead to hospitalization is treated as a fixed value, which will allow us to see how different values affect the model. The concentration parameter for the negative binomial noise model is also fixed. In practice, both of these parameters would be given a somewhat informative prior and then inferred.

Code

# Infection-hospitalization ratio (1% of infections lead to hospitalization)
ihr_rv = DeterministicVariable("ihr", 0.01)

# Overdispersion parameter for negative binomial
concentration_rv = DeterministicVariable("concentration", 10.0)

# Create the observation process
hosp_process = Counts(
    name="hospital",
    ascertainment_rate_rv=ihr_rv,
    delay_distribution_rv=delay_rv,
    noise=NegativeBinomialNoise(concentration_rv),
)

Timeline alignment and lookback period

The observation process convolves infections with a delay distribution, maintaining alignment between input and output: day \(t\) in the output corresponds to day \(t\) in the input.

Hospital admissions depend on infections from prior days. A delay PMF of length \(L\) covers delays 0 to \(L-1\), requiring \(L-1\) days of prior infection history. The method lookback_days() returns \(L-1\); the first valid observation day is at index lookback_days(). Earlier days are marked invalid.

Code

print(f"Required lookback: {hosp_process.lookback_days()} days")


def first_valid_observation_day(obs_process) -> int:
    """Return the first day index with complete infection history for convolution."""
    return obs_process.lookback_days()

Required lookback: 54 days

Simulating observed hospital admissions given a single day’s worth of infections

To demonstrate how a Counts observation process works, we examine how infections occurring on a single day result in observed hospital admissions.

Code

n_days = 100
day_one = first_valid_observation_day(hosp_process)

# Create infections with a spike
infection_spike_day = day_one + 10
infections = jnp.zeros(n_days)
infections = infections.at[infection_spike_day].set(2000)

We plot the infections starting from day_one (the first valid observation day, after the lookback period).

Code

# Plot relative to first valid observation day
n_plot_days = n_days - day_one
rel_spike_day = infection_spike_day - day_one

infections_df = pd.DataFrame(
    {
        "day": np.arange(n_plot_days),
        "count": np.array(infections[day_one:]),
    }
)

max_infection_count = float(jnp.max(infections[day_one:]))

plot_infections = (
    p9.ggplot(infections_df, p9.aes(x="day", y="count"))
    + p9.geom_line(color="darkblue", size=1)
    + p9.geom_point(color="darkblue", size=2)
    + p9.geom_vline(
        xintercept=rel_spike_day,
        color="darkred",
        linetype="dashed",
        alpha=0.5,
    )
    + p9.labs(x="Day", y="Daily Infections", title="Infections (Input)")
    + p9.theme_grey()
    + p9.theme(plot_title=p9.element_text(size=13, weight="bold"))
    + p9.annotate(
        "text",
        x=rel_spike_day + 2,
        y=max_infection_count * 0.9,
        label=f"Infection spike (day {rel_spike_day})",
        color="darkred",
        size=10,
    )
)
plot_infections

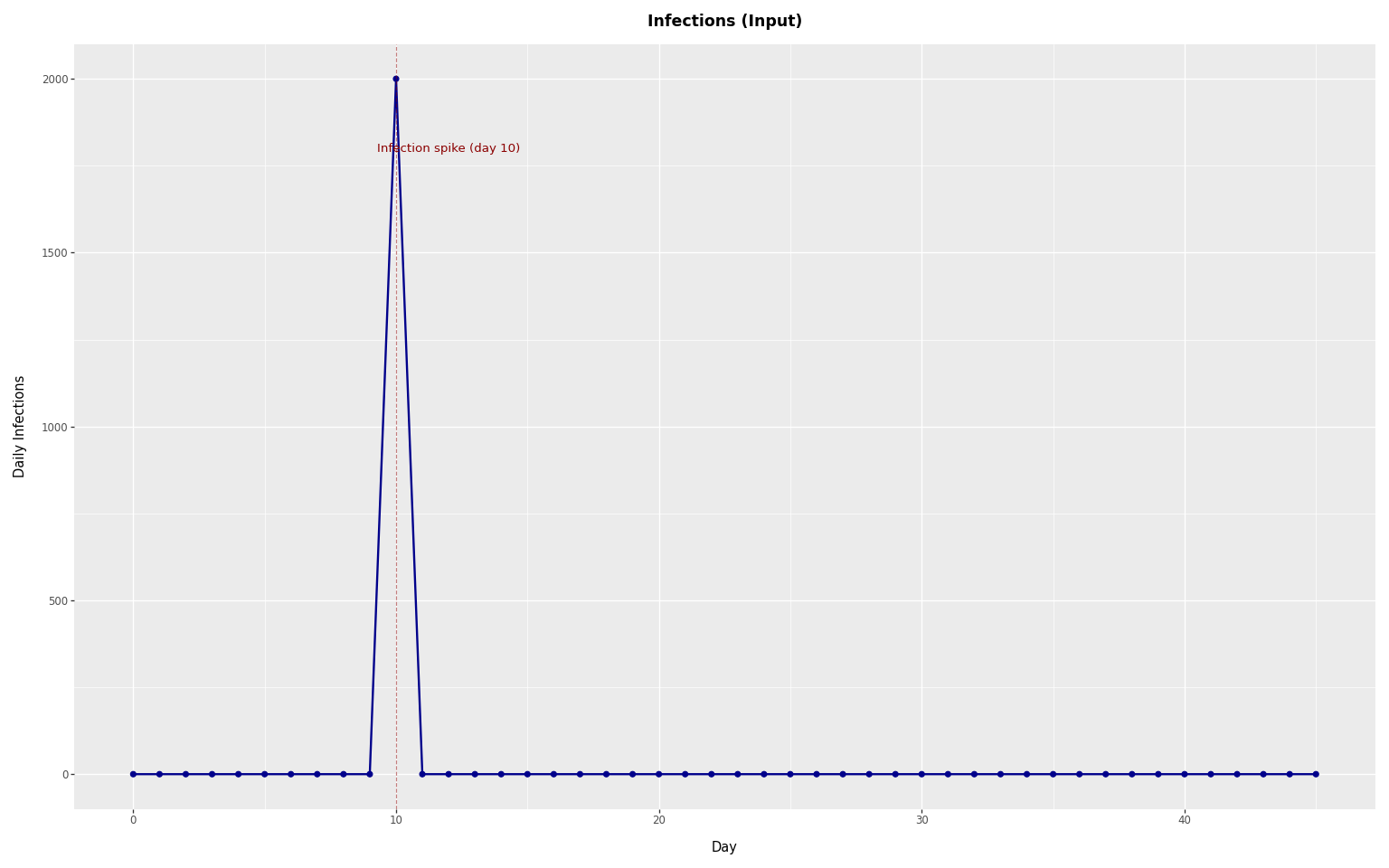
Because all infections occur on a single day, this allows us to see how one day’s worth of infections result in hospital admissions spread over subsequent days according to the delay distribution.

Predicted admissions without observation noise.

First, we compute the predicted admissions from the convolution alone, without observation noise. This is the mean of the distribution from which samples are drawn.

Code

# Compute predicted admissions (convolution only, no observation noise)
from pyrenew.convolve import compute_delay_ascertained_incidence

# Scale infections by IHR (ascertainment rate)
infections_scaled = infections * float(ihr_rv.sample())
predicted_admissions, offset = compute_delay_ascertained_incidence(
    p_observed_given_incident=1.0,
    latent_incidence=infections_scaled,
    delay_incidence_to_observation_pmf=hosp_delay_pmf,
    pad=True,
)

Code

# Relative peak day for plotting
peak_day = rel_spike_day + mode_delay

# Plot predicted admissions (x-axis: day_one = first valid observation day)
predicted_df = pd.DataFrame(
    {
        "day": np.arange(n_plot_days),
        "admissions": np.array(predicted_admissions[day_one:]),
    }
)

max_predicted = float(predicted_df["admissions"].max())
plot_predicted = (
    p9.ggplot(predicted_df, p9.aes(x="day", y="admissions"))
    + p9.geom_line(color="purple", size=1)
    + p9.geom_point(color="purple", size=1.5)
    + p9.geom_vline(
        xintercept=rel_spike_day,
        color="darkred",
        linetype="dashed",
        alpha=0.5,
    )
    + p9.geom_vline(
        xintercept=peak_day,
        color="purple",
        linetype="dashed",
        alpha=0.5,
    )
    + p9.labs(
        x="Day",
        y="Hospital Admissions",
        title="Predicted Hospital Admissions (Deterministic)",
    )
    + p9.theme_grey()
    + p9.annotate(
        "text",
        x=rel_spike_day,
        y=max_predicted * 1.05,
        label=f"Infection spike\n(day {rel_spike_day})",
        color="darkred",
        size=9,
        ha="center",
    )
    + p9.annotate(
        "text",
        x=peak_day,
        y=max_predicted * 1.05,
        label=f"Peak\n(day {peak_day})",
        color="purple",
        size=9,
        ha="center",
    )
)
plot_predicted

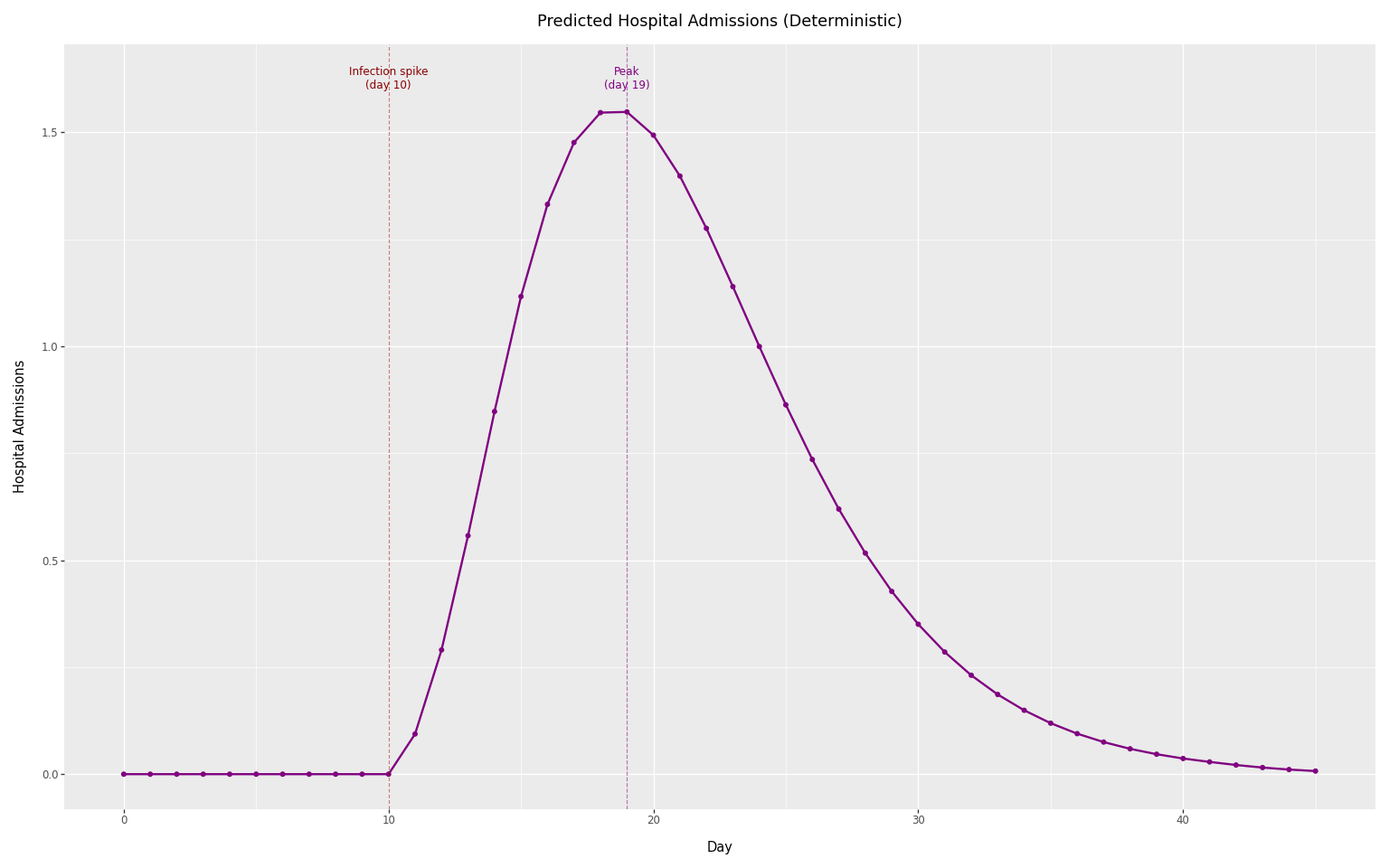
The predicted admissions mirror the delay distribution, shifted by the infection spike day and scaled by the IHR.

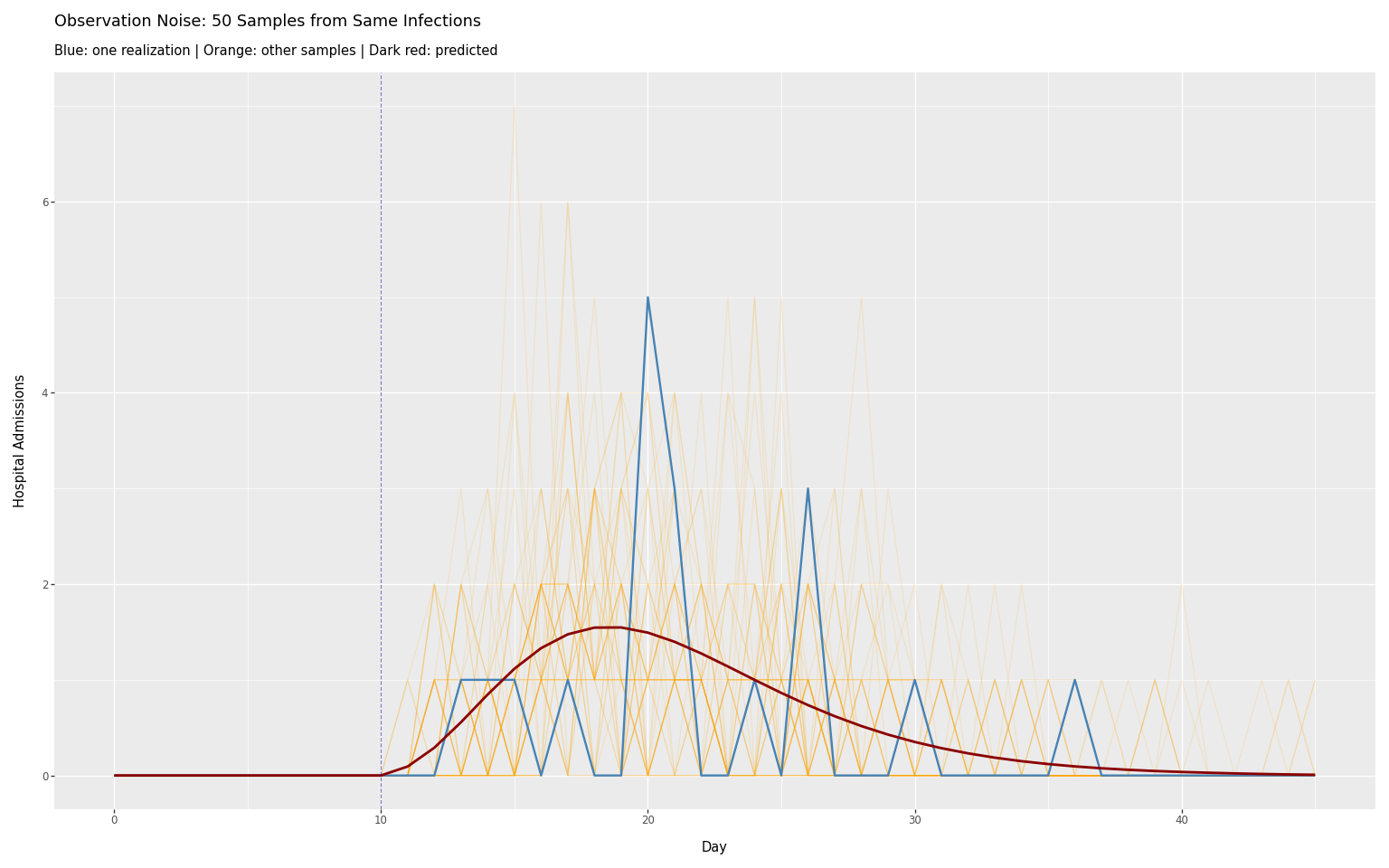
Observation Noise (Negative Binomial)

The negative binomial distribution adds stochastic variation. Sampling multiple times from the same infections shows the range of possible observations:

Code

# Sample 50 realizations of hospital admissions from the same infection spike
n_samples = 50
samples_list = []

for seed in range(n_samples):
    with numpyro.handlers.seed(rng_seed=seed):
        hosp_sample = hosp_process.sample(infections=infections, obs=None)

    # Slice from day_one to align with valid observation period
    for i, val in enumerate(hosp_sample.observed[day_one:]):
        samples_list.append(
            {
                "day": i,
                "admissions": float(val),
                "sample": seed,
                "type": "sampled",
            }
        )

# Add predicted values
for i, val in enumerate(predicted_admissions[day_one:]):
    samples_list.append(
        {
            "day": i,
            "admissions": float(val),
            "sample": -1,
            "type": "predicted",
        }
    )

Code

samples_df = pd.DataFrame(samples_list)
sampled_df = samples_df[samples_df["type"] == "sampled"]
predicted_noise_df = samples_df[samples_df["type"] == "predicted"]

# Separate one sample to highlight
highlight_sample = 0
other_samples_df = sampled_df[sampled_df["sample"] != highlight_sample]
highlight_df = sampled_df[sampled_df["sample"] == highlight_sample]

plot_50_samples = (
    p9.ggplot()
    + p9.geom_line(
        p9.aes(x="day", y="admissions", group="sample"),
        data=other_samples_df,
        color="orange",
        alpha=0.15,
        size=0.5,
    )
    + p9.geom_line(
        p9.aes(x="day", y="admissions"),
        data=highlight_df,
        color="steelblue",
        size=1,
    )
    + p9.geom_line(
        p9.aes(x="day", y="admissions"),
        data=predicted_noise_df,
        color="darkred",
        size=1.2,
    )
    + p9.geom_vline(
        xintercept=rel_spike_day,
        color="darkblue",
        linetype="dashed",
        alpha=0.5,
    )
    + p9.labs(
        x="Day",
        y="Hospital Admissions",
        title=f"Observation Noise: {n_samples} Samples from Same Infections",
        subtitle="Blue: one realization | Orange: other samples | Dark red: predicted",
    )
    + p9.theme_grey()
)
plot_50_samples

Code

# Print timeline statistics
print("Timeline Analysis:")
print(
    f"  Infection spike on day {rel_spike_day}: {infections[infection_spike_day]:.0f} people"
)
print(f"  Mode delay from infection to hospitalization: {mode_delay} days")
print(
    f"  Predicted hospitalization peak: day {rel_spike_day + mode_delay} (= {rel_spike_day} + {mode_delay})"
)

Timeline Analysis:
  Infection spike on day 10: 2000 people
  Mode delay from infection to hospitalization: 9 days
  Predicted hospitalization peak: day 19 (= 10 + 9)

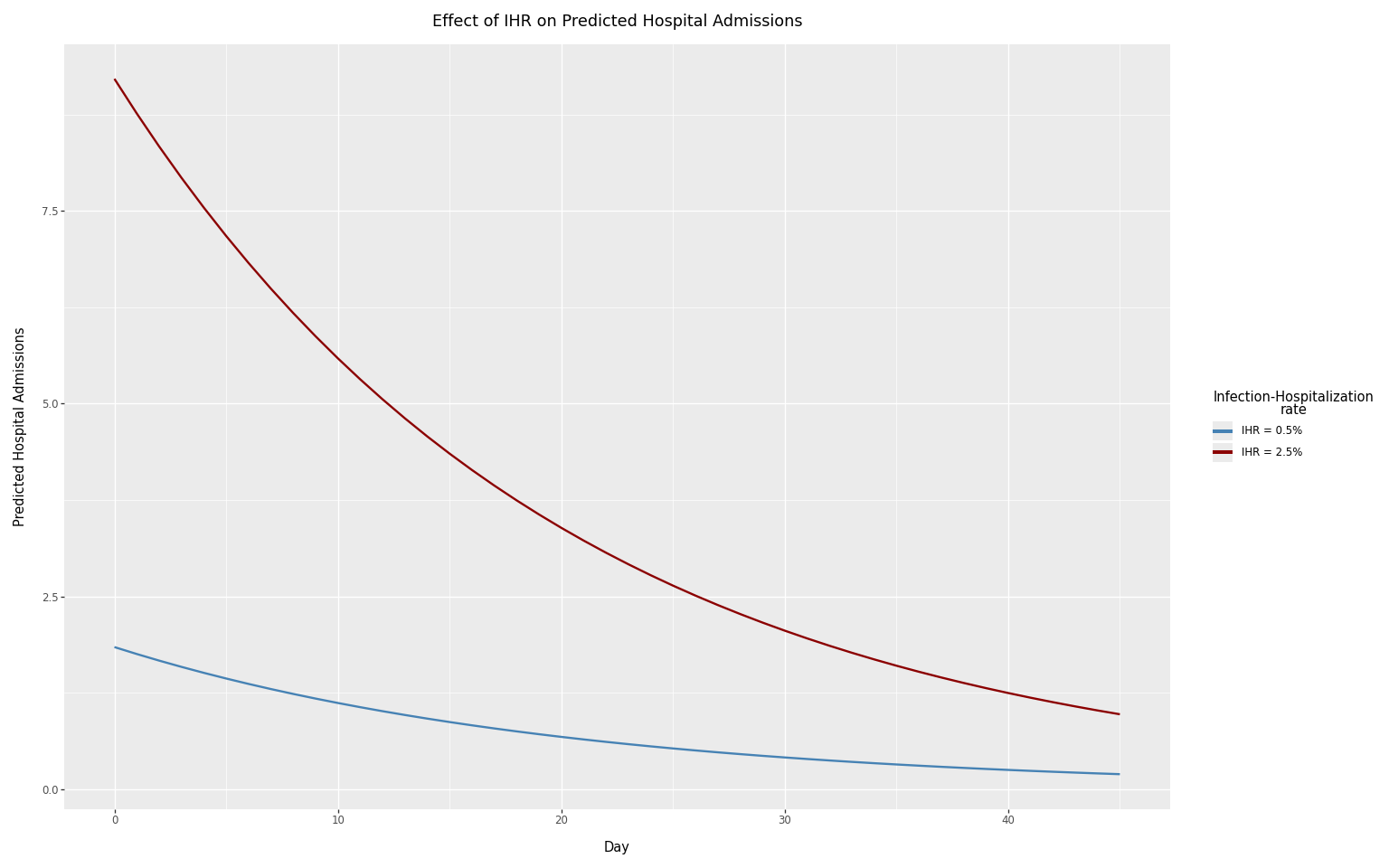
Effect of the ascertainment rate

The ascertainment rate (here, the infection-hospitalization rate or IHR) directly scales the number of predicted hospital admissions. We compare two contrasting IHR values: 0.5% and 2.5%.

Code

# Two contrasting IHR values
ihr_values = [0.005, 0.025]
peak_value = 3000  # Peak infections
infections_decay = peak_value * jnp.exp(-jnp.arange(n_days) / 20.0)

# Compute predicted hospital admissions (no noise) for each IHR
results_list = []
for ihr_val in ihr_values:
    infections_scaled = infections_decay * ihr_val
    predicted_hosp, _ = compute_delay_ascertained_incidence(
        p_observed_given_incident=1.0,
        latent_incidence=infections_scaled,
        delay_incidence_to_observation_pmf=hosp_delay_pmf,
        pad=True,
    )

    for i, admit in enumerate(predicted_hosp[day_one:]):
        results_list.append(
            {
                "day": i,
                "admissions": float(admit),
                "IHR": f"IHR = {ihr_val:.1%}",
            }
        )

Code

results_df = pd.DataFrame(results_list)

plot_ihr = (
    p9.ggplot(results_df, p9.aes(x="day", y="admissions", color="IHR"))
    + p9.geom_line(size=1)
    + p9.scale_color_manual(values=["steelblue", "darkred"])
    + p9.labs(
        x="Day",
        y="Predicted Hospital Admissions",
        title="Effect of IHR on Predicted Hospital Admissions",
        color="Infection-Hospitalization\nrate",
    )
    + p9.theme_grey()
)
plot_ihr

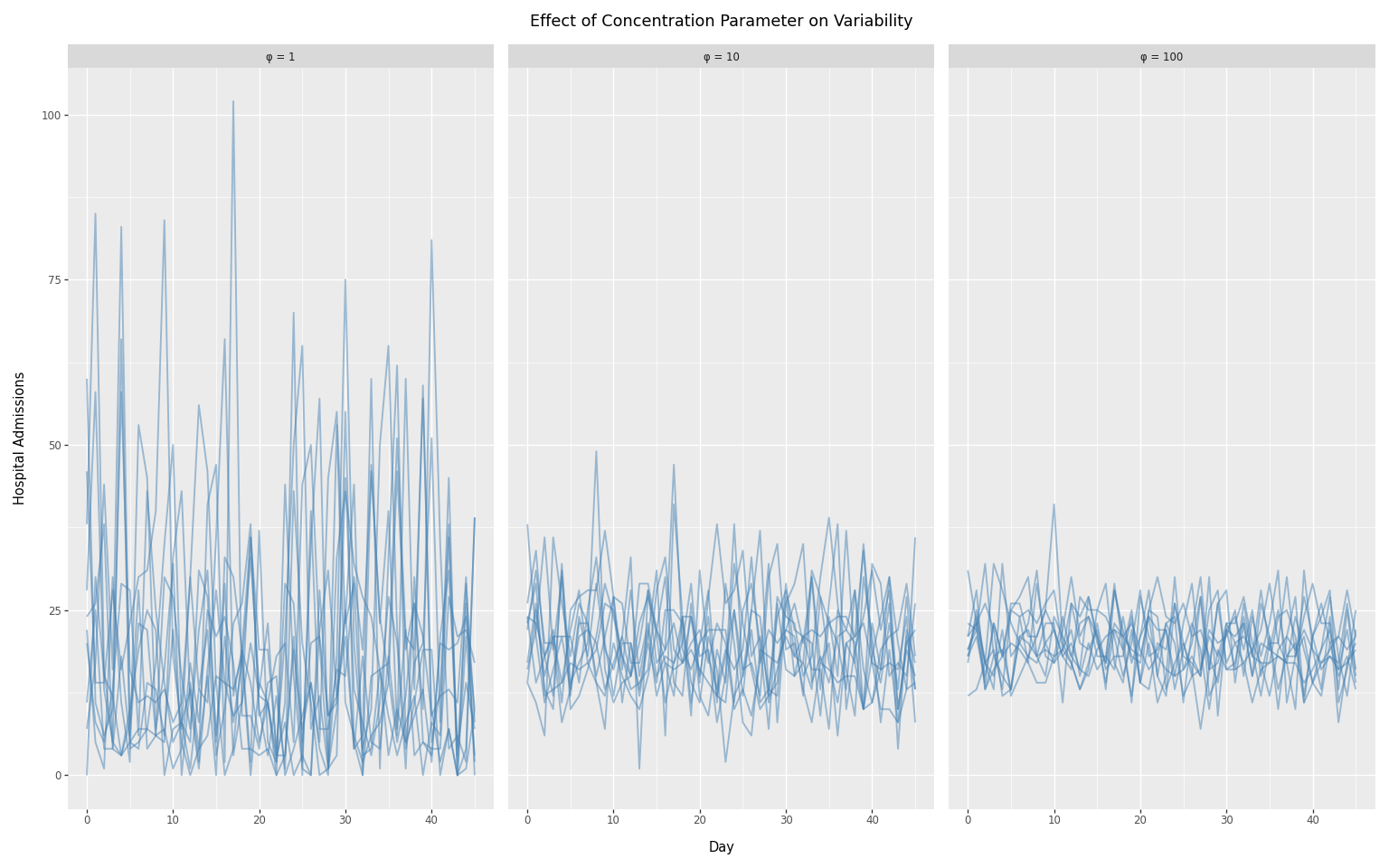
Negative binomial concentration parameter

The concentration parameter \(\phi\) controls overdispersion:

• Higher \(\phi\) → less overdispersion (approaches Poisson)
• Lower \(\phi\) → more overdispersion (noisier data)

We compare three concentration values spanning two orders of magnitude:

• φ = 1: high overdispersion (noisy)
• φ = 10: moderate overdispersion
• φ = 100: nearly Poisson (minimal noise)

Code

# Use constant infections
peak_value = 2000
infections_constant = peak_value * jnp.ones(n_days)

# Concentration values spanning two orders of magnitude
concentration_values = [1.0, 10.0, 100.0]
n_replicates = 10

# Collect results
conc_results = []
for conc_val in concentration_values:
    conc_rv_temp = DeterministicVariable("conc", conc_val)
    process_temp = Counts(
        name="hospital",
        ascertainment_rate_rv=ihr_rv,
        delay_distribution_rv=delay_rv,
        noise=NegativeBinomialNoise(conc_rv_temp),
    )

    for seed in range(n_replicates):
        with numpyro.handlers.seed(rng_seed=seed):
            hosp_temp = process_temp.sample(
                infections=infections_constant,
                obs=None,
            )

        # Slice from day_one to align with valid observation period
        for i, admit in enumerate(hosp_temp.observed[day_one:]):
            conc_results.append(
                {
                    "day": i,
                    "admissions": float(admit),
                    "concentration": f"φ = {int(conc_val)}",
                    "replicate": seed,
                }
            )

Code

conc_df = pd.DataFrame(conc_results)

# Convert to ordered categorical
conc_df["concentration"] = pd.Categorical(
    conc_df["concentration"],
    categories=["φ = 1", "φ = 10", "φ = 100"],
    ordered=True,
)

plot_concentration = (
    p9.ggplot(conc_df, p9.aes(x="day", y="admissions", group="replicate"))
    + p9.geom_line(alpha=0.5, size=0.8, color="steelblue")
    + p9.facet_wrap("~ concentration", ncol=3)
    + p9.labs(
        x="Day",
        y="Hospital Admissions",
        title="Effect of Concentration Parameter on Variability",
    )
    + p9.theme_grey()
)
plot_concentration

Swapping noise models

To use Poisson noise instead of negative binomial, change the noise model:

Code

hosp_process_poisson = Counts(
    name="hospital",
    ascertainment_rate_rv=ihr_rv,
    delay_distribution_rv=delay_rv,
    noise=PoissonNoise(),
)

with numpyro.handlers.seed(rng_seed=42):
    poisson_result = hosp_process_poisson.sample(
        infections=infections,
        obs=None,
    )

print(
    f"Sampled {len(poisson_result.observed)} days of hospital admissions with Poisson noise"
)

Sampled 100 days of hospital admissions with Poisson noise

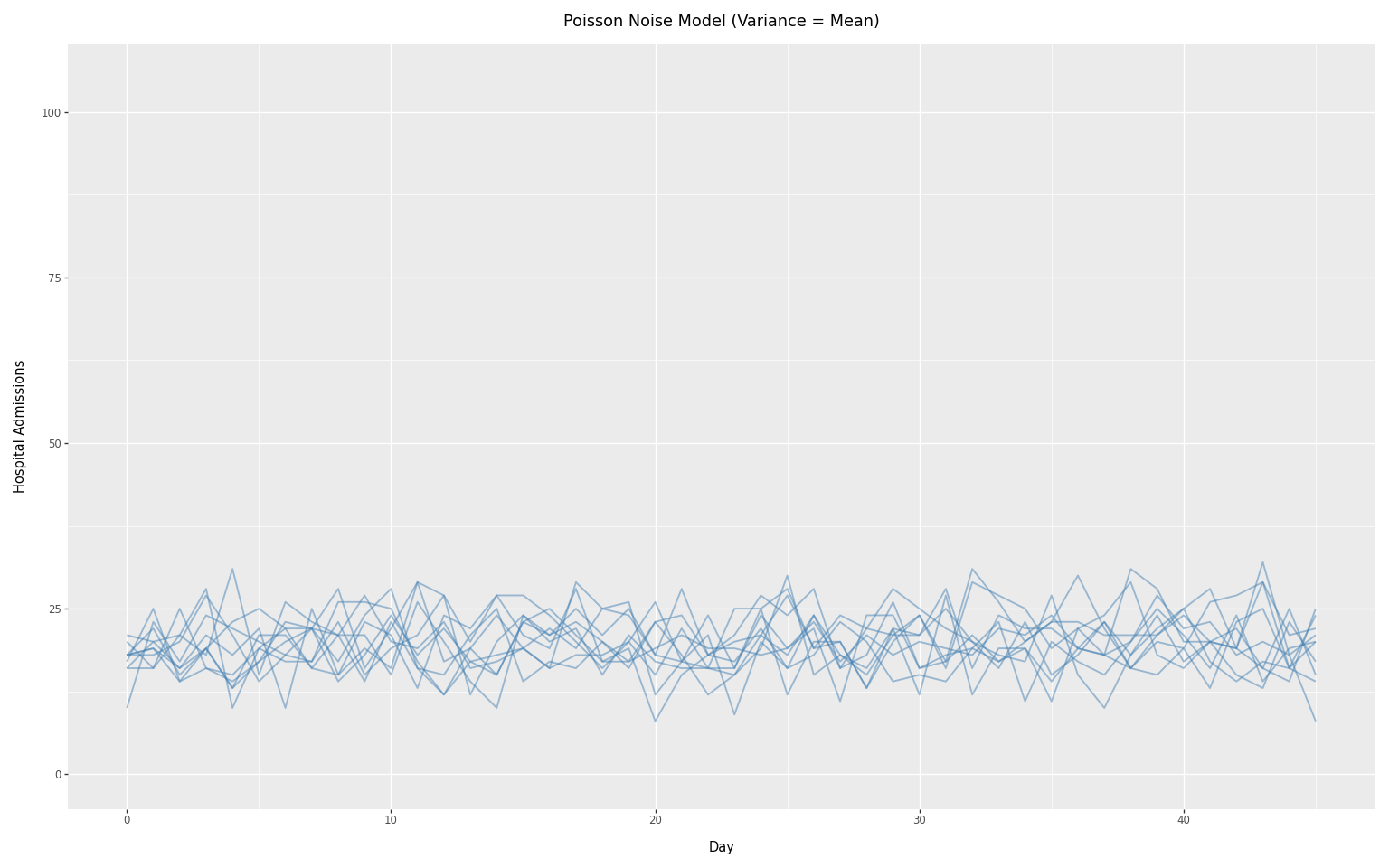
We can visualize the Poisson noise model using the same constant infection scenario as the concentration comparison above. Since Poisson assumes variance equals the mean, it produces less variability than the negative binomial with low concentration values.

To see the reduction in noise, it is necessary to keep the y-axis on the same scale as in the previous plot.

Code

# Sample multiple realizations with Poisson noise
n_replicates_poisson = 10

poisson_results = []
for seed in range(n_replicates_poisson):
    with numpyro.handlers.seed(rng_seed=seed):
        poisson_temp = hosp_process_poisson.sample(
            infections=infections_constant,
            obs=None,
        )

    # Slice from day_one to align with valid observation period
    for i, admit in enumerate(poisson_temp.observed[day_one:]):
        poisson_results.append(
            {
                "day": i,
                "admissions": float(admit),
                "replicate": seed,
            }
        )
poisson_df = pd.DataFrame(poisson_results)

plot_poisson = (
    p9.ggplot(poisson_df, p9.aes(x="day", y="admissions", group="replicate"))
    + p9.geom_line(alpha=0.5, size=0.8, color="steelblue")
    + p9.labs(
        x="Day",
        y="Hospital Admissions",
        title="Poisson Noise Model (Variance = Mean)",
    )
    + p9.theme_grey()
    + p9.ylim(0, 105)
)
plot_poisson