Hierarchical Latent Infections: Understanding Temporal Process Choices

Code

import jax.numpy as jnp
import jax.random as random
import numpy as np
import numpyro
from numpyro.infer import Predictive
import pandas as pd
import plotnine as p9
import warnings

warnings.filterwarnings("ignore")

Code

from pyrenew.latent import (
    HierarchicalInfections,
    AR1,
    DifferencedAR1,
    RandomWalk,
)
from pyrenew.deterministic import DeterministicPMF, DeterministicVariable

The Modeling Problem

You have a jurisdiction (e.g., a state or metropolitan area) with multiple subpopulations. Some subpopulations have direct observations; others do not. Disaggregated data from many subpopulations is often both sparse and noisy. You want to model transmission dynamics that:

• Share information across subpopulations (pooling strength)
• Allow local transmission to deviate from the jurisdiction average
• Produce estimates for both observed and unobserved areas

HierarchicalInfections addresses this by decomposing the effective reproduction number \(\mathcal{R}(t)\) into:

\[\log \mathcal{R}_k(t) = \log \mathcal{R}_{\text{baseline}}(t) + \delta_k(t)\]

where:

• \(\mathcal{R}_{\text{baseline}}(t)\) is the jurisdiction-level reproduction number (shared across all subpopulations)
• \(\delta_k(t)\) is the deviation for subpopulation \(k\), constrained so that \(\sum_k \delta_k(t) = 0\)

The sum-to-zero constraint ensures \(\mathcal{R}_{\text{baseline}}(t)\) represents the geometric mean of subpopulation \(\mathcal{R}\) values—a natural “center” for the hierarchy.

Each subpopulation runs its own renewal equation with its own \(\mathcal{R}_k(t)\), then results are aggregated for jurisdiction-level quantities (like total hospital admissions).

Model Inputs

HierarchicalInfections requires several inputs that shape the infection dynamics. Understanding what each does helps you configure the model appropriately.

A Note on RandomVariables

All inputs to HierarchicalInfections are RandomVariables—objects that can be sampled. In this tutorial, we use DeterministicVariable and DeterministicPMF (fixed values) for clarity. In real inference, you would typically use DistributionalVariable with priors for quantities you want to estimate (like I0 or initial Rt).

For example:

# Fixed value (for illustration)
I0_rv = DeterministicVariable("I0", 0.001)

# With a prior (for inference)
from pyrenew.randomvariable import DistributionalVariable
import numpyro.distributions as dist
I0_rv = DistributionalVariable("I0", dist.Beta(1, 1000))

Population Structure

We define subpopulations as fractions of the total jurisdiction population:

Code

# 6 subpopulations with their population fractions
# Which subpopulations are "observed" or "unobserved" is determined by each
# observation process (via subpop_indices), not by the latent process.
subpop_fractions = jnp.array([0.10, 0.14, 0.21, 0.22, 0.07, 0.26])

n_subpops = len(subpop_fractions)
print(f"Number of subpopulations: {n_subpops}")
print(f"Total population fraction: {float(jnp.sum(subpop_fractions)):.2f}")

Number of subpopulations: 6
Total population fraction: 1.00

Note: Population structure is passed at sample time, not when constructing the process. This allows the same model specification to be fit to different jurisdictions.

Generation Interval

The generation interval is the probability distribution over the time between infection of a primary case and infection of a secondary case. It determines the “memory” of the renewal process—how current infections depend on past infections.

Code

# Typical COVID-like generation interval
gen_int_pmf = jnp.array([0.16, 0.32, 0.25, 0.14, 0.07, 0.04, 0.02])
gen_int_rv = DeterministicPMF("gen_int", gen_int_pmf)

days = np.arange(len(gen_int_pmf))
mean_gen_time = float(np.sum(days * gen_int_pmf))
print(f"Mean generation time: {mean_gen_time:.1f} days")

Mean generation time: 1.8 days

What it controls: The generation interval affects how quickly infection dynamics respond to changes in Rt:

• Shorter generation interval → faster response, more volatile dynamics
• Longer generation interval → slower response, smoother dynamics

The generation interval is typically fixed based on pathogen biology, not estimated from data.

Code

# Compare generation intervals: short vs long
gi_short = jnp.array([0.4, 0.4, 0.2])  # Mean ~1 day
gi_long = jnp.array([0.05, 0.1, 0.2, 0.3, 0.2, 0.1, 0.05])  # Mean ~3.5 days

gi_short_rv = DeterministicPMF("gi_short", gi_short)
gi_long_rv = DeterministicPMF("gi_long", gi_long)

print(
    f"Short GI mean: {float(np.sum(np.arange(len(gi_short)) * gi_short)):.1f} days"
)
print(
    f"Long GI mean: {float(np.sum(np.arange(len(gi_long)) * gi_long)):.1f} days"
)

Short GI mean: 0.8 days
Long GI mean: 3.0 days

To illustrate, we sample infection trajectories using each generation interval while holding other inputs fixed (I0 = 0.001, DifferencedAR1 baseline, AR1 deviations) and using the same random seed so the underlying Rt trajectory is identical. Solid lines use initial_log_rt = 0 (Rt starts at 1); dashed lines show initial_log_rt = ±0.2 (Rt starts growing or declining) with the standard GI:

Code

# Create models with different generation intervals
baseline_rt_process = DifferencedAR1(autoreg=0.9, innovation_sd=0.05)
subpop_rt_deviation_process = AR1(autoreg=0.8, innovation_sd=0.05)

n_days_demo = 28
gi_data = []

# GI comparison at initial_log_rt = 0
gi_configs = {
    "Short GI (~1 day)": gi_short_rv,
    "Standard GI (~2 days)": gen_int_rv,
    "Long GI (~3.5 days)": gi_long_rv,
}

# Use consistent n_initialization_points across all GI configs
# so the temporal process trajectories are comparable (same seed → same Rt)
n_init_gi = max(len(rv()) for rv in gi_configs.values())

for name, gi_rv in gi_configs.items():
    model = HierarchicalInfections(
        gen_int_rv=gi_rv,
        I0_rv=DeterministicVariable("I0", 0.001),
        initial_log_rt_rv=DeterministicVariable("initial_log_rt", 0.0),
        baseline_rt_process=baseline_rt_process,
        subpop_rt_deviation_process=subpop_rt_deviation_process,
        n_initialization_points=n_init_gi,
    )
    with numpyro.handlers.seed(rng_seed=42):
        inf_agg, _ = model.sample(
            n_days_post_init=n_days_demo,
            subpop_fractions=subpop_fractions,
        )
    n_init = model.n_initialization_points
    inf = np.array(inf_agg)[n_init:]
    for d in range(len(inf)):
        gi_data.append(
            {
                "day": d,
                "infections": float(inf[d]),
                "config": name,
                "linetype": "solid",
            }
        )

# initial_log_rt comparison with standard GI
for init_rt_name, init_rt_val in [
    ("Rt≈1.22 (growing)", 0.2),
    ("Rt≈0.82 (declining)", -0.2),
]:
    model = HierarchicalInfections(
        gen_int_rv=gen_int_rv,
        I0_rv=DeterministicVariable("I0", 0.001),
        initial_log_rt_rv=DeterministicVariable("initial_log_rt", init_rt_val),
        baseline_rt_process=baseline_rt_process,
        subpop_rt_deviation_process=subpop_rt_deviation_process,
        n_initialization_points=n_init_gi,
    )
    with numpyro.handlers.seed(rng_seed=42):
        inf_agg, _ = model.sample(
            n_days_post_init=n_days_demo,
            subpop_fractions=subpop_fractions,
        )
    n_init = model.n_initialization_points
    inf = np.array(inf_agg)[n_init:]
    for d in range(len(inf)):
        gi_data.append(
            {
                "day": d,
                "infections": float(inf[d]),
                "config": f"Standard GI, {init_rt_name}",
                "linetype": "dashed",
            }
        )

gi_df = pd.DataFrame(gi_data)

(
    p9.ggplot(
        gi_df,
        p9.aes(x="day", y="infections", color="config", linetype="config"),
    )
    + p9.geom_line(size=1)
    + p9.scale_linetype_manual(
        values={
            "Short GI (~1 day)": "solid",
            "Standard GI (~2 days)": "solid",
            "Long GI (~3.5 days)": "solid",
            "Standard GI, Rt≈1.22 (growing)": "dashed",
            "Standard GI, Rt≈0.82 (declining)": "dashed",
        }
    )
    + p9.labs(
        x="Days",
        y="Infections (proportion)",
        title="Effect of Generation Interval and Initial Rt",
        color="Configuration",
        linetype="Configuration",
    )
    + p9.theme_minimal()
    + p9.theme(figure_size=(10, 5), legend_position="right")
)

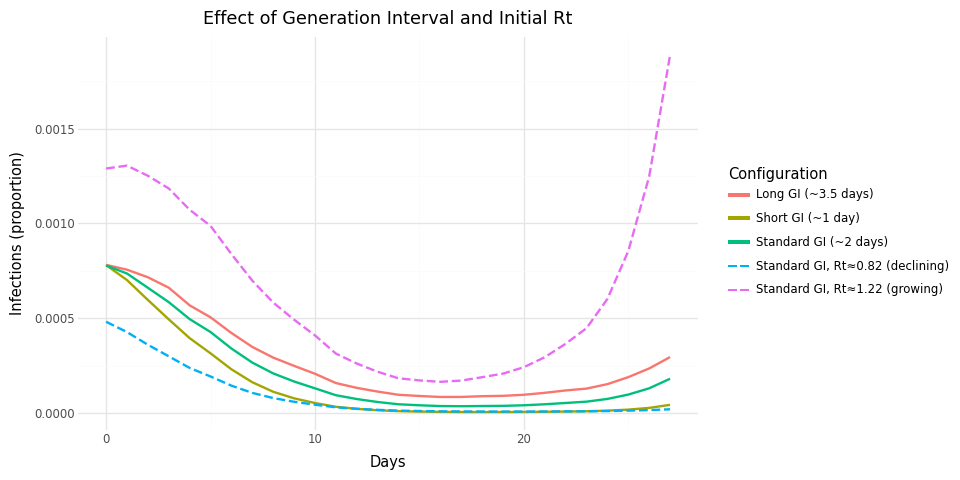
Figure 1: Effect of generation interval and initial_log_rt on infection dynamics. Solid lines start at Rt=1; dashed lines show initial growth (Rt≈1.22) or decline (Rt≈0.82).

Code

gi_df_zoom = gi_df[(gi_df["day"] >= 14) & (gi_df["day"] <= 21)]

(
    p9.ggplot(
        gi_df_zoom,
        p9.aes(x="day", y="infections", color="config", linetype="config"),
    )
    + p9.geom_line(size=1)
    + p9.scale_linetype_manual(
        values={
            "Short GI (~1 day)": "solid",
            "Standard GI (~2 days)": "solid",
            "Long GI (~3.5 days)": "solid",
            "Standard GI, Rt≈1.22 (growing)": "dashed",
            "Standard GI, Rt≈0.82 (declining)": "dashed",
        }
    )
    + p9.labs(
        x="Days",
        y="Infections (proportion)",
        title="Zoomed: Days 14-21",
        color="Configuration",
        linetype="Configuration",
    )
    + p9.theme_minimal()
    + p9.theme(figure_size=(10, 5), legend_position="right")
)

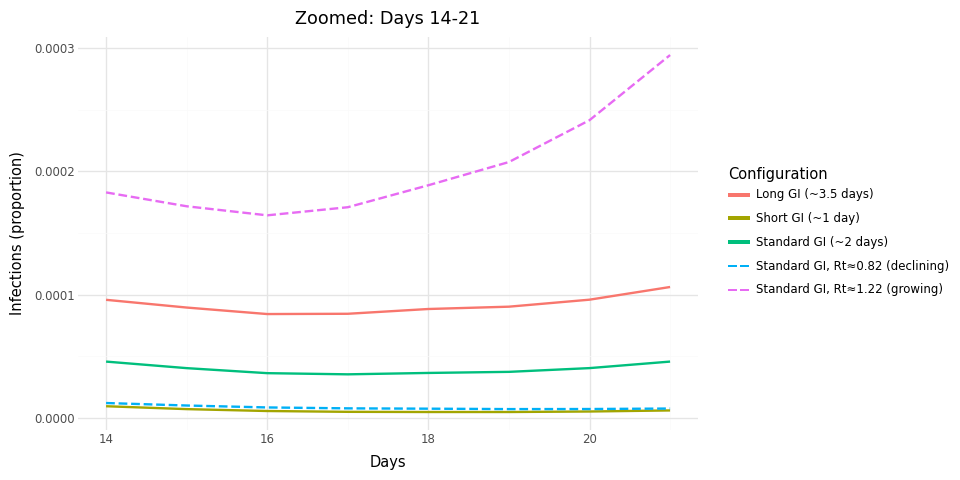
Figure 2: Zoomed view of days 14-21 showing separation between trajectories.

Initial Conditions: I0 and initial_log_rt

Parameters I0 and initial_log_rt set the starting point for the infection process.

The previous plot shows the effect of initial_log_rt: the solid lines use initial_log_rt = 0 (Rt starts at 1), while the dashed lines use initial_log_rt = ±0.2 (Rt starts above or below 1). Notice that the solid lines stay flat for the first ~15 days — when Rt = 1, each infected person infects approximately one other, so infection levels remain stable. The dashed lines show immediate growth or decline because Rt starts away from 1.

The flat period for solid lines also reflects DifferencedAR1 with high autoregression (0.9): this process models the rate of change of log(Rt), starting from zero, and changes accumulate gradually. If you need more initial dynamics, set initial_log_rt ≠ 0, use RandomWalk instead, or increase innovation_sd.

I0 is the proportion of the population infected at time zero. It seeds the renewal equation and scales the entire trajectory:

Code

# Default values
I0_rv = DeterministicVariable("I0", 0.001)  # 0.1% initially infected
initial_log_rt_rv = DeterministicVariable(
    "initial_log_rt", 0.0
)  # Rt starts at 1.0

print(f"I0 = 0.001 means {0.001:.1%} of population initially infected")
print(f"initial_log_rt = 0.0 means Rt starts at {np.exp(0.0):.1f}")

I0 = 0.001 means 0.1% of population initially infected
initial_log_rt = 0.0 means Rt starts at 1.0

In the previous plot, I0 was specified as: I0_rv=DeterministicVariable("I0", 0.001), i.e., \(0.1%\) of the population. We overplot trajectories for \(10%\) and \(0.01%\) as well.

Code

i0_configs = {
    "I0 = 0.0001 (0.01%)": 0.0001,
    "I0 = 0.001 (0.1%)": 0.001,
    "I0 = 0.01 (1%)": 0.01,
}

i0_results = {}
for name, i0_val in i0_configs.items():
    model = HierarchicalInfections(
        gen_int_rv=gen_int_rv,
        I0_rv=DeterministicVariable("I0", i0_val),
        initial_log_rt_rv=DeterministicVariable("initial_log_rt", 0.0),
        baseline_rt_process=baseline_rt_process,
        subpop_rt_deviation_process=subpop_rt_deviation_process,
        n_initialization_points=len(gen_int_pmf),
    )
    with numpyro.handlers.seed(rng_seed=42):
        inf_agg, _ = model.sample(
            n_days_post_init=n_days_demo,
            subpop_fractions=subpop_fractions,
        )
    n_init = model.n_initialization_points
    i0_results[name] = np.array(inf_agg)[n_init:]

i0_data = []
for name, inf in i0_results.items():
    for d in range(len(inf)):
        i0_data.append({"day": d, "infections": float(inf[d]), "I0": name})
i0_df = pd.DataFrame(i0_data)

(
    p9.ggplot(i0_df, p9.aes(x="day", y="infections", color="I0"))
    + p9.geom_line(size=1)
    + p9.scale_y_log10()
    + p9.labs(
        x="Days",
        y="Infections (proportion, log scale)",
        title="Effect of Initial Infection Prevalence (I0)",
        subtitle="Same Rt trajectory, different starting prevalence",
    )
    + p9.theme_minimal()
    + p9.theme(figure_size=(10, 5))
)

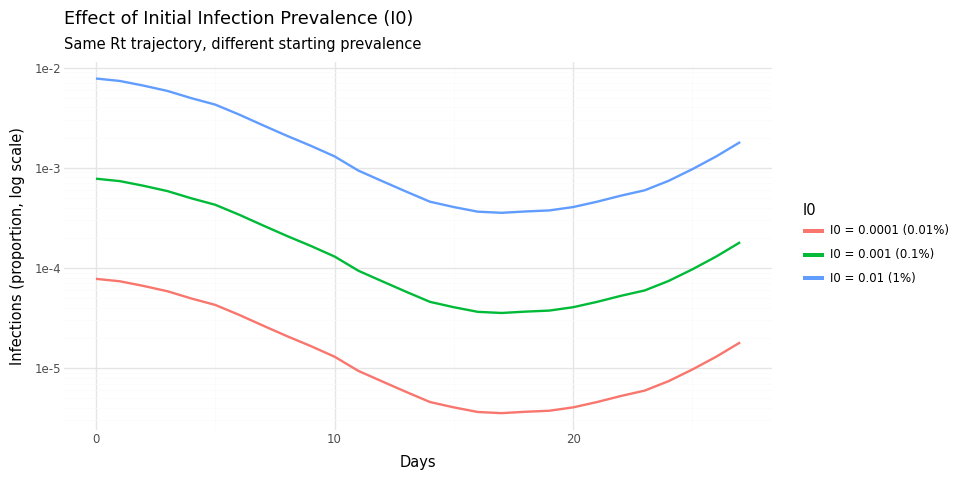
Figure 3: Effect of I0 on infection scale. Higher I0 shifts the entire trajectory up proportionally.

Temporal Processes

The temporal process determines how \(\mathcal{R}_{\text{baseline}}(t)\) and the deviations \(\delta_k(t)\) evolve over time. PyRenew provides three options:

Process	What It Does	Epidemiological Interpretation
RandomWalk	Each value = previous + noise	Maximum flexibility; Rt can drift anywhere
AR1	Each value reverts toward a mean	Rt stays bounded near a baseline; deviations decay
DifferencedAR1	The rate of change reverts toward zero	Rt can trend persistently, but growth rate stabilizes

Choosing a temporal process:

If you believe…	Consider
Rt should stay near 1 (endemic equilibrium)	AR1 for baseline
Rt may trend up/down over your horizon	DifferencedAR1 for baseline
Local differences are transient	AR1 for deviations
Local differences persist	RandomWalk for deviations

Parameters:

• autoreg (AR1, DifferencedAR1): How strongly the process reverts. Values near 1 = slow reversion; near 0 = fast.
• innovation_sd: Daily volatility. Larger values = more variable trajectories.

Configuring the Latent Process

Now let’s assemble all the inputs:

Code

# Baseline Rt: DifferencedAR1 allows trends while stabilizing growth rate
baseline_rt_process = DifferencedAR1(autoreg=0.9, innovation_sd=0.05)

# Subpopulation deviations: AR1 shrinks differences back toward zero
subpop_rt_deviation_process = AR1(autoreg=0.8, innovation_sd=0.05)

Why these choices?

• DifferencedAR1 for baseline: We don’t want to force Rt back to 1; epidemics can grow or decline persistently. But we do want the rate of change to stabilize.
• AR1 for deviations: We expect local differences to be somewhat transient. If one area has a temporary spike, it should eventually return toward the jurisdiction average.

Creating the Process

Code

latent_infections = HierarchicalInfections(
    gen_int_rv=gen_int_rv,
    I0_rv=I0_rv,
    initial_log_rt_rv=initial_log_rt_rv,
    baseline_rt_process=baseline_rt_process,
    subpop_rt_deviation_process=subpop_rt_deviation_process,
    n_initialization_points=len(gen_int_pmf),
)

print(
    f"Generation interval length: {latent_infections.get_required_lookback()} days"
)
print(
    f"Initialization points: {latent_infections.n_initialization_points} days"
)

Generation interval length: 7 days
Initialization points: 7 days

Prior Predictive Checks: What Does the Model Believe?

Now we examine what infection dynamics this configuration considers plausible—before seeing any data.

Single Sample

Code

n_days = 28  # 4 weeks of simulation

with numpyro.handlers.seed(rng_seed=42):
    result = latent_infections.sample(
        n_days_post_init=n_days,
        subpop_fractions=subpop_fractions,
    )

infections_agg, infections_all = result

n_total = infections_agg.shape[0]
n_init = n_total - n_days

print("Output shapes:")
print(f"  Aggregate (jurisdiction total): {infections_agg.shape}")
print(f"  All subpopulations: {infections_all.shape}")
print(
    f"\nTimeline: {n_init} initialization days + {n_days} simulation days = {n_total} total"
)

Output shapes:
  Aggregate (jurisdiction total): (35,)
  All subpopulations: (35, 6)

Timeline: 7 initialization days + 28 simulation days = 35 total

Many Samples: The Prior Predictive Distribution

A single sample tells us little. We need many samples to understand the distribution of trajectories the model considers plausible.

Code

def sample_model():
    """Wrapper for prior predictive sampling."""
    return latent_infections.sample(
        n_days_post_init=n_days,
        subpop_fractions=subpop_fractions,
    )


n_samples = 200
predictive = Predictive(sample_model, num_samples=n_samples)
prior_samples = predictive(random.PRNGKey(42))

print(
    f"Rt baseline samples: {prior_samples['latent_infections/rt_baseline'].shape}"
)
print(
    f"Infection samples: {prior_samples['latent_infections/infections_aggregate'].shape}"
)

Rt baseline samples: (200, 35, 1)
Infection samples: (200, 35)

Visualizing the Prior: Baseline Rt Trajectories

Code

# Extract post-initialization Rt trajectories
rt_samples = np.array(prior_samples["latent_infections/rt_baseline"])[
    :, n_init:, 0
]

# Build long-format dataframe for plotting
rt_data = []
for i in range(n_samples):
    for d in range(n_days):
        rt_data.append({"day": d, "rt": float(rt_samples[i, d]), "sample": i})
rt_df = pd.DataFrame(rt_data)

# Compute summary statistics
rt_median = np.median(rt_samples, axis=0)
rt_mean = np.mean(rt_samples, axis=0)
rt_q05 = np.percentile(rt_samples, 5, axis=0)
rt_q95 = np.percentile(rt_samples, 95, axis=0)

Code

# Cap display for readability (some trajectories explode)
rt_cap = 5.0
n_extreme = np.sum(np.any(rt_samples > rt_cap, axis=1))

(
    p9.ggplot(rt_df, p9.aes(x="day", y="rt", group="sample"))
    + p9.geom_line(alpha=0.1, size=0.4, color="steelblue")
    + p9.geom_hline(yintercept=1.0, color="red", linetype="dashed", alpha=0.7)
    + p9.scale_x_continuous(expand=(0, 0))
    + p9.coord_cartesian(ylim=(0, rt_cap))
    + p9.labs(
        x="Days",
        y="Rt (baseline)",
        title=f"Prior Predictive: Baseline Rt ({n_samples} samples)",
        subtitle=f"Red dashed line: Rt = 1. {n_extreme} samples exceed Rt = {rt_cap} (not shown in full).",
    )
    + p9.theme_minimal()
)

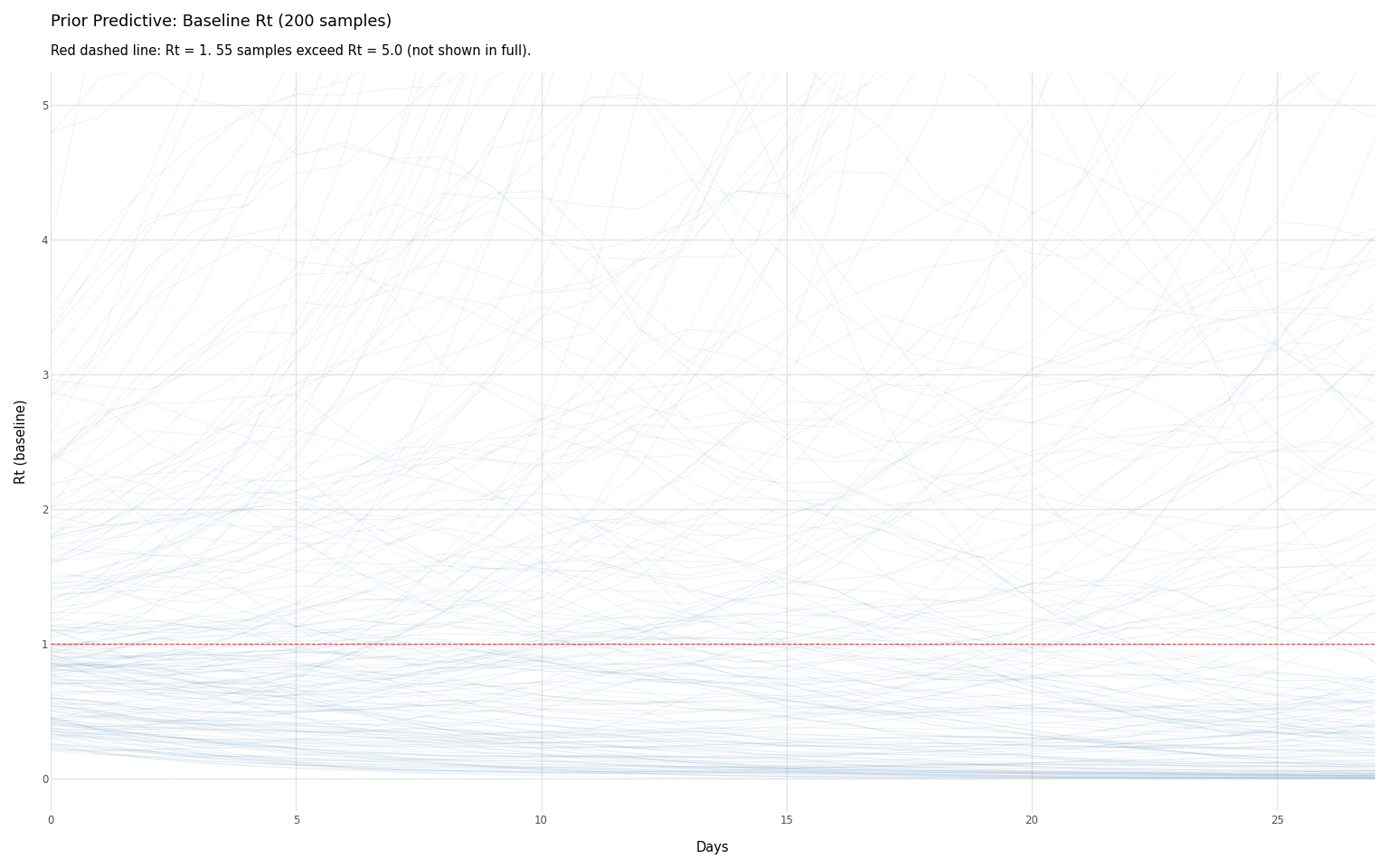
Figure 4: Prior predictive distribution of baseline Rt. Each light blue line is one sample from the prior. The model considers all these trajectories plausible before seeing data.

Interpreting the Prior Predictive

Code

print("Rt at end of simulation (day 28):")
print(f"  5th percentile:  {rt_q05[-1]:.2f}")
print(f"  Median:          {rt_median[-1]:.2f}")
print(f"  Mean:            {rt_mean[-1]:.2f}")
print(f"  95th percentile: {rt_q95[-1]:.2f}")
print(f"  Maximum:         {np.max(rt_samples[:, -1]):.1f}")

Rt at end of simulation (day 28):
  5th percentile:  0.01
  Median:          0.82
  Mean:            9.68
  95th percentile: 41.50
  Maximum:         364.0

What this tells us:

The median stays near 1, but the mean is pulled up by explosive trajectories. This is a consequence of modeling on the log scale:

• Half the trajectories have Rt \< 1 (bounded below by 0)
• Half have Rt > 1 (unbounded above—can reach 10, 50, 100+)
• The explosive trajectories dominate the mean

Is this a problem? It depends on your data. With abundant data, these extreme trajectories will be ruled out by the likelihood. With sparse data, they may not be—and your posterior could include implausible dynamics.

Comparing Temporal Process Choices

The prior predictive distribution changes dramatically based on your temporal process choices. Let’s compare the three options for baseline Rt.

Code

temporal_configs = {
    "AR(1)": AR1(autoreg=0.9, innovation_sd=0.05),
    "DifferencedAR1": DifferencedAR1(autoreg=0.5, innovation_sd=0.05),
    "RandomWalk": RandomWalk(innovation_sd=0.05),
}

process_samples = {}
for name, temporal in temporal_configs.items():
    model = HierarchicalInfections(
        gen_int_rv=gen_int_rv,
        I0_rv=I0_rv,
        initial_log_rt_rv=initial_log_rt_rv,
        baseline_rt_process=temporal,
        subpop_rt_deviation_process=AR1(autoreg=0.8, innovation_sd=0.05),
        n_initialization_points=len(gen_int_pmf),
    )

    def make_sampler(m):
        return lambda: m.sample(
            n_days_post_init=n_days,
            subpop_fractions=subpop_fractions,
        )

    samples = Predictive(make_sampler(model), num_samples=n_samples)(
        random.PRNGKey(42)
    )
    process_samples[name] = np.array(samples["latent_infections/rt_baseline"])[
        :, n_init:, 0
    ]

Code

# Build comparison dataframe
comparison_data = []
for name, rt in process_samples.items():
    for i in range(n_samples):
        for d in range(n_days):
            comparison_data.append(
                {
                    "day": d,
                    "rt": float(rt[i, d]),
                    "sample": i,
                    "process": name,
                }
            )
comparison_df = pd.DataFrame(comparison_data)
comparison_df["process"] = pd.Categorical(
    comparison_df["process"],
    categories=["AR(1)", "DifferencedAR1", "RandomWalk"],
    ordered=True,
)

Code

(
    p9.ggplot(comparison_df, p9.aes(x="day", y="rt", group="sample"))
    + p9.geom_line(alpha=0.1, size=0.4, color="steelblue")
    + p9.geom_hline(yintercept=1.0, color="red", linetype="dashed", alpha=0.7)
    + p9.facet_wrap("~ process", ncol=3)
    + p9.scale_x_continuous(expand=(0, 0))
    + p9.coord_cartesian(ylim=(0, 3.0))
    + p9.labs(
        x="Days",
        y="Rt (baseline)",
        title="Prior Predictive by Temporal Process",
        subtitle="Same innovation_sd=0.05; AR(1) autoreg=0.9, DifferencedAR1 autoreg=0.5",
    )
    + p9.theme_minimal()
    + p9.theme(figure_size=(12, 4))
)

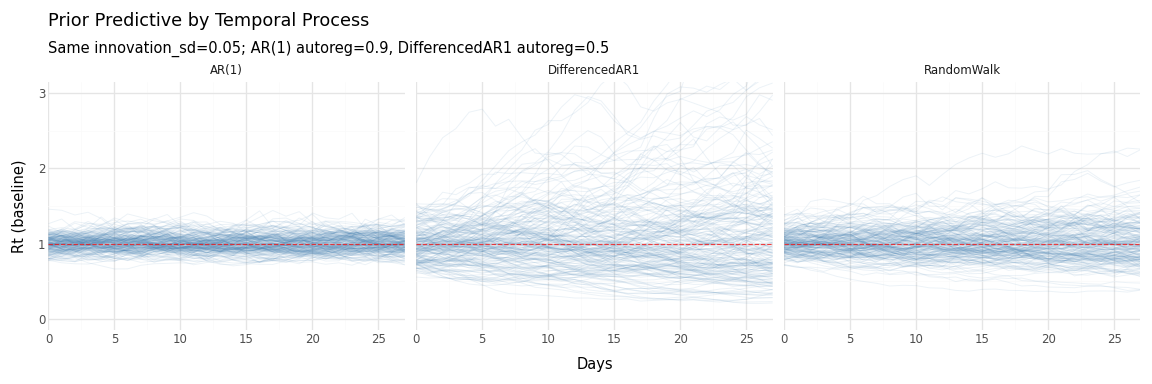
Figure 5: Effect of temporal process choice on prior Rt trajectories. AR(1) stays bounded near 1; DifferencedAR1 and RandomWalk can drift further.

Code

print("Rt at day 28 by temporal process:")
print(f"{'Process':<18} {'Median':>8} {'Mean':>8} {'95th %':>8} {'Max':>8}")
print("-" * 52)
for name in ["AR(1)", "DifferencedAR1", "RandomWalk"]:
    rt = process_samples[name][:, -1]
    print(
        f"{name:<18} {np.median(rt):>8.2f} {np.mean(rt):>8.2f} "
        f"{np.percentile(rt, 95):>8.2f} {np.max(rt):>8.1f}"
    )

Rt at day 28 by temporal process:
Process              Median     Mean   95th %      Max
----------------------------------------------------
AR(1)                  1.01     1.01     1.23      1.3
DifferencedAR1         1.04     1.16     2.44      3.9
RandomWalk             0.99     1.02     1.51      2.3

Key observations:

• AR(1) produces the tightest distribution—Rt reverts toward 1
• DifferencedAR1 allows more drift but growth rate stabilizes
• RandomWalk has the widest spread—no mean reversion at all

Subpopulation Deviations

The same choice applies to subpopulation deviations \(\delta_k(t)\). Let’s compare AR(1) vs RandomWalk:

Code

subpop_configs = {
    "AR(1) deviations": AR1(autoreg=0.8, innovation_sd=0.05),
    "RandomWalk deviations": RandomWalk(innovation_sd=0.05),
}

deviation_samples = {}
for name, subpop_rt_deviation_process in subpop_configs.items():
    model = HierarchicalInfections(
        gen_int_rv=gen_int_rv,
        I0_rv=I0_rv,
        initial_log_rt_rv=initial_log_rt_rv,
        baseline_rt_process=DifferencedAR1(autoreg=0.9, innovation_sd=0.05),
        subpop_rt_deviation_process=subpop_rt_deviation_process,
        n_initialization_points=len(gen_int_pmf),
    )

    def make_sampler(m):
        return lambda: m.sample(
            n_days_post_init=n_days,
            subpop_fractions=subpop_fractions,
        )

    deviation_samples[name] = Predictive(
        make_sampler(model), num_samples=n_samples
    )(random.PRNGKey(42))

Code

# Plot deviations for first subpopulation
dev_data = []
for name in subpop_configs.keys():
    devs = np.array(
        deviation_samples[name]["latent_infections/subpop_deviations"]
    )[:, n_init:, 0]
    for i in range(n_samples):
        for d in range(n_days):
            dev_data.append(
                {
                    "day": d,
                    "deviation": float(devs[i, d]),
                    "sample": i,
                    "process": name,
                }
            )
dev_df = pd.DataFrame(dev_data)

Code

(
    p9.ggplot(dev_df, p9.aes(x="day", y="deviation", group="sample"))
    + p9.geom_line(alpha=0.15, size=0.4, color="purple")
    + p9.geom_hline(yintercept=0, color="black", linetype="dotted")
    + p9.facet_wrap("~ process", ncol=2)
    + p9.scale_x_continuous(expand=(0, 0))
    + p9.labs(
        x="Days",
        y="Deviation δ₁(t)",
        title="Subpopulation Deviation Trajectories (first subpop)",
        subtitle=f"{n_samples} prior samples; baseline uses DifferencedAR1",
    )
    + p9.theme_minimal()
    + p9.theme(figure_size=(10, 4))
)

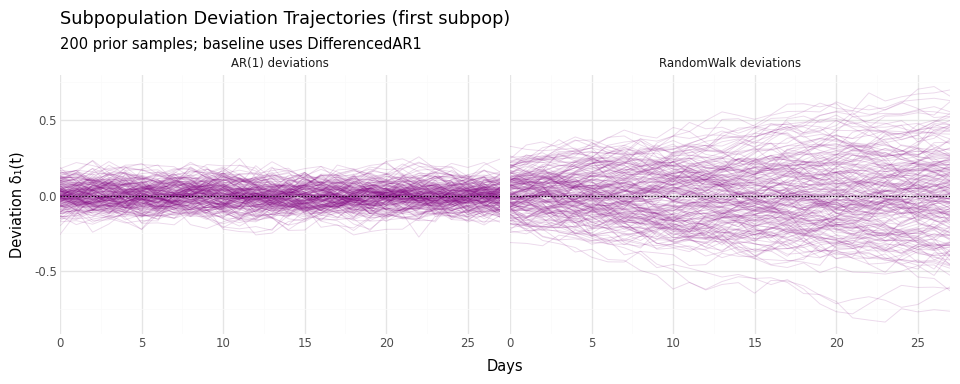
Figure 6: Subpopulation deviations under different temporal processes. AR(1) deviations decay toward zero; RandomWalk deviations can diverge.

Interpretation:

• AR(1) deviations stay close to zero—subpopulations track the jurisdiction average
• RandomWalk deviations can grow—subpopulations can diverge substantially

Choose based on your scientific question: Do you expect local differences to persist or decay?

Tuning Hyperparameters

The autoreg and innovation_sd parameters control how constrained the prior is. Let’s compare a “weakly informative” vs “more informative” configuration:

Code

configs = {
    "Weakly informative\n(autoreg=0.9, sd=0.05)": {
        "baseline": DifferencedAR1(autoreg=0.9, innovation_sd=0.05),
        "subpop": AR1(autoreg=0.8, innovation_sd=0.05),
    },
    "More informative\n(autoreg=0.7, sd=0.02)": {
        "baseline": DifferencedAR1(autoreg=0.7, innovation_sd=0.02),
        "subpop": AR1(autoreg=0.6, innovation_sd=0.02),
    },
}

tuning_samples = {}
for name, cfg in configs.items():
    model = HierarchicalInfections(
        gen_int_rv=gen_int_rv,
        I0_rv=I0_rv,
        initial_log_rt_rv=initial_log_rt_rv,
        baseline_rt_process=cfg["baseline"],
        subpop_rt_deviation_process=cfg["subpop"],
        n_initialization_points=len(gen_int_pmf),
    )

    def make_sampler(m):
        return lambda: m.sample(
            n_days_post_init=n_days,
            subpop_fractions=subpop_fractions,
        )

    tuning_samples[name] = Predictive(
        make_sampler(model), num_samples=n_samples
    )(random.PRNGKey(42))

Code

# Build comparison dataframe
tuning_data = []
for name, samples in tuning_samples.items():
    rt = np.array(samples["latent_infections/rt_baseline"])[:, n_init:, 0]
    for i in range(n_samples):
        for d in range(n_days):
            tuning_data.append(
                {
                    "day": d,
                    "rt": float(rt[i, d]),
                    "sample": i,
                    "config": name,
                }
            )
tuning_df = pd.DataFrame(tuning_data)

Code

(
    p9.ggplot(tuning_df, p9.aes(x="day", y="rt", group="sample"))
    + p9.geom_line(alpha=0.1, size=0.4, color="steelblue")
    + p9.geom_hline(yintercept=1.0, color="red", linetype="dashed", alpha=0.7)
    + p9.facet_wrap("~ config", ncol=2)
    + p9.scale_x_continuous(expand=(0, 0))
    + p9.coord_cartesian(ylim=(0, 3.0))
    + p9.labs(
        x="Days",
        y="Rt (baseline)",
        title="Effect of Hyperparameter Tuning",
    )
    + p9.theme_minimal()
    + p9.theme(figure_size=(10, 4))
)

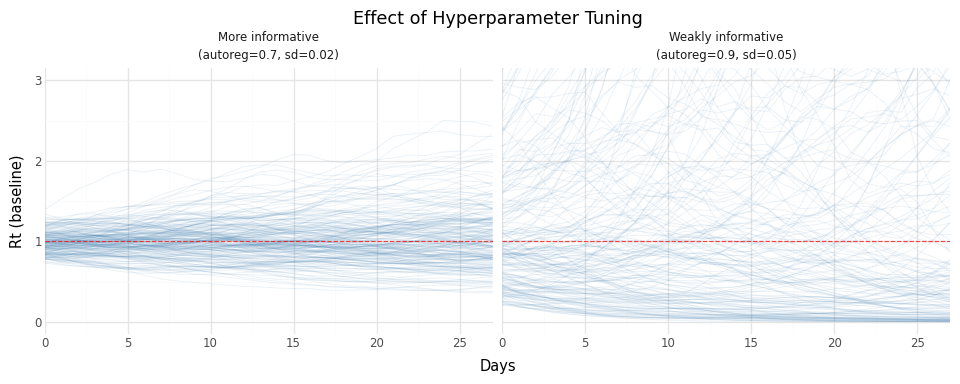
Figure 7: Effect of hyperparameter choices on prior Rt distribution. Tighter parameters produce more constrained trajectories.

Guidance:

• Lower autoreg → faster reversion → tighter distribution
• Lower innovation_sd → smaller daily changes → smoother trajectories
• With sparse data, more informative priors prevent explosive estimates
• With abundant data, weakly informative priors let the data speak

Verifying Model Structure

Before using HierarchicalInfections in a full model, verify the hierarchical structure is working correctly:

Code

# Check that deviations sum to zero (identifiability constraint)
with numpyro.handlers.seed(rng_seed=123):
    with numpyro.handlers.trace() as trace:
        latent_infections.sample(
            n_days_post_init=n_days,
            subpop_fractions=subpop_fractions,
        )

deviations = trace["latent_infections/subpop_deviations"]["value"]
deviation_sums = jnp.sum(deviations, axis=1)
print(
    f"Max |sum of deviations|: {float(jnp.max(jnp.abs(deviation_sums))):.2e}"
)
print("(Should be ~0 due to sum-to-zero constraint)")

Max |sum of deviations|: 2.98e-08
(Should be ~0 due to sum-to-zero constraint)

Code

# Check that aggregate = weighted sum of subpopulations
with numpyro.handlers.seed(rng_seed=123):
    inf_agg, inf_all = latent_infections.sample(
        n_days_post_init=n_days,
        subpop_fractions=subpop_fractions,
    )

computed_agg = jnp.sum(inf_all * subpop_fractions[None, :], axis=1)
max_diff = float(jnp.max(jnp.abs(computed_agg - inf_agg)))

print(f"Max difference (aggregate vs weighted sum): {max_diff:.2e}")
print(
    "Hierarchical structure verified!"
    if max_diff < 1e-5
    else "ERROR: Mismatch detected"
)

Max difference (aggregate vs weighted sum): 0.00e+00
Hierarchical structure verified!

Summary

What We Covered

1. HierarchicalInfections models subpopulation structure with shared baseline Rt and local deviations

2. Model inputs each affect the dynamics differently:

   • Generation interval: Determines response speed (fixed by pathogen biology)
   • I0: Scales the entire infection trajectory
   • initial_log_rt: Sets initial growth/decline direction
   • Temporal processes: Control how Rt evolves over time

3. All inputs are RandomVariables: In inference, use DistributionalVariable with priors for quantities you want to estimate

4. Prior predictive checks reveal model beliefs before seeing data—critical when data is sparse or noisy

Decision Guide

Input	Consideration
Generation interval	Fixed by pathogen; shorter = faster dynamics
I0	Often poorly identified; prior matters
initial_log_rt	Sets starting direction; can often be estimated
Temporal process	AR1 for regularization; RandomWalk for flexibility
autoreg, innovation_sd	Lower values = tighter prior; adjust if trajectories explode

Code Summary

from pyrenew.latent import HierarchicalInfections, AR1, DifferencedAR1
from pyrenew.deterministic import DeterministicPMF, DeterministicVariable

# Configure the latent process
latent = HierarchicalInfections(
    gen_int_rv=DeterministicPMF("gen_int", gen_int_pmf),
    I0_rv=DeterministicVariable("I0", 0.001),
    initial_log_rt_rv=DeterministicVariable("initial_log_rt", 0.0),
    baseline_rt_process=DifferencedAR1(autoreg=0.9, innovation_sd=0.05),
    subpop_rt_deviation_process=AR1(autoreg=0.8, innovation_sd=0.05),
    n_initialization_points=len(gen_int_pmf),
)

# Sample (population structure provided at sample time)
infections_agg, infections_all = latent.sample(
    n_days_post_init=28,
    subpop_fractions=subpop_fractions,
)

When building the full multisignal model, you would instantiate a PyrenewBuilder object and call the configure_latent method to specify the latent process model structure: generation interval, initial infections, and temporal dynamics. See tutorial:

• Building Multi-Signal Renewal Models