Building Multi-Signal Renewal Models
Code
import numpyro
# to run samplers in parallel you must run `set_host_device_count` before importing jax
numpyro.set_host_device_count(4)
numpyro.enable_x64()
Code
import arviz as az
import jax
import jax.numpy as jnp
import jax.random as random
import numpy as np
import numpyro.distributions as dist
import plotnine as p9
import pandas as pd
import time
import warnings
warnings.filterwarnings("ignore")
from _tutorial_theme import theme_tutorial
def make_rng_key():
"""Generate a time-based random seed."""
seed = int(time.time() * 1000) % (2**32)
return random.PRNGKey(seed)
/home/runner/work/PyRenew/PyRenew/.venv/lib/python3.14/site-packages/arviz/__init__.py:50: FutureWarning:
ArviZ is undergoing a major refactor to improve flexibility and extensibility while maintaining a user-friendly interface.
Some upcoming changes may be backward incompatible.
For details and migration guidance, visit: https://python.arviz.org/en/latest/user_guide/migration_guide.html
warn(
Code
from jax.typing import ArrayLike
from pyrenew import datasets
from pyrenew.deterministic import (
DeterministicPMF,
DeterministicVariable,
)
from pyrenew.metaclass import RandomVariable
from pyrenew.randomvariable import DistributionalVariable
from pyrenew.latent import (
HierarchicalInfections,
AR1,
RandomWalk,
GammaGroupSdPrior,
HierarchicalNormalPrior,
)
from pyrenew.model import PyrenewBuilder
from pyrenew.observation import (
Counts,
HierarchicalNormalNoise,
Measurements,
MeasurementNoise,
NegativeBinomialNoise,
)
Overview
Renewal models in PyRenew combine two types of components:
-
Latent infection process: Generates unobserved infections via the renewal equation, driven by a time-varying reproduction number \(\mathcal{R}(t)\)
-
Observation processes: Transform latent infections into observable signals (hospital admissions, wastewater concentrations, etc.) by applying delays, ascertainment, and noise
A multi-signal model combines multiple observation processes—each representing a different data stream, e.g., hospital admissions, wastewater concentrations, which stem from the same underlying latent infection process. By jointly modeling these signals, we can improve estimation and prediction of the time-varying reproduction number \(\mathcal{R}(t)\). Such a model must:
- Generate a single coherent infection trajectory (or set of trajectories for subpopulations)
- Route those infections to each observation process appropriately
- Handle the initialization period required by delay distributions
The PyrenewBuilder class handles this plumbing. You specify:
- A latent process (e.g.,
HierarchicalInfections) that defines how infections evolve - One or more observation processes (e.g.,
Counts,Measurements) that define how infections become data
The builder computes initialization requirements, wires components together, and produces a model ready for inference.
Related Tutorials
Before diving into multi-signal models, you may want to review these foundational tutorials:
- Hierarchical Latent Infections: Understanding temporal process choices for \(\mathcal{R}(t)\)
- Observation Processes: Counts: Modeling count data (admissions, deaths)
- Observation Processes: Measurements: Modeling continuous data (wastewater)
This tutorial shows how to combine these components into a complete multi-signal model.
What This Tutorial Covers
This tutorial demonstrates building a multi-signal renewal model using:
HierarchicalInfections— subpopulations share a jurisdiction-level baseline \(\mathcal{R}(t)\) with subpopulation-specific deviationsCounts— hospital admissions (jurisdiction-level)- A custom
Wastewaterclass — viral concentrations (subpopulation-level)
Model Structure
In this tutorial, we build a model that jointly fits two data streams to a shared latent infection process:
- Hospital admissions — jurisdiction-level counts that reflect total infections across all subpopulations, delayed and underascertained
- Wastewater concentrations — site-level measurements from a subset of subpopulations (catchment areas), reflecting viral shedding and dilution
The diagram below shows how data flows through the model. The latent process generates infection trajectories for all subpopulations. Each observation process receives the infections it needs — aggregated totals or per-subpopulation arrays — and transforms them into predicted observations via delays, ascertainment, shedding kinetics, and noise.
flowchart TB
subgraph Latent["Latent Infection Process"]
L["Renewal equation<br/>(HierarchicalInfections)"]
end
subgraph Infections["Infection Trajectories"]
J["Jurisdiction total<br/>(summed across subpopulations)"]
S["Per-subpopulation infections<br/>(all subpopulations)"]
end
subgraph Obs["Observation Processes"]
C["Hospital admissions<br/>(Counts)"]
W["Wastewater concentrations<br/>(Measurements)"]
end
subgraph Data["Observed Data"]
HA["Reported admissions"]
WW["Measured viral concentrations"]
end
L --> S
S -->|"weighted sum"| J
J --> C
S -->|"select monitored subpopulations"| W
C -->|"delay + ascertainment + noise"| HA
W -->|"shedding + dilution + noise"| WWInfection Resolution
Different observation processes observe different levels of the model hierarchy. Each observation process declares an infection resolution that determines what infection data it receives:
| Resolution | Receives | Example signals |
|---|---|---|
"aggregate" |
Aggregated infections (sum across all subpopulations), shape (T,) |
Hospital admissions, case counts |
"subpop" |
Infection matrix for all subpopulations, shape (T, n_subpops) |
Wastewater, site-specific surveillance |
The PyrenewBuilder routes latent infections to observation processes
based on each process’s declared resolution.
For subpopulation-level observations, the observation process selects
which subpopulations it observes using subpop_indices provided at
sample/fit time. This allows flexible observation patterns—for example,
wastewater samples might only cover 5 of 6 subpopulations (catchment
areas), while the 6th represents areas without wastewater monitoring.
With this structure in mind, we’ll now define each component following the generative direction: first the latent infection process, then the observation processes.
Latent Infection Process
Latent infection processes implement the renewal equation to generate infection trajectories. All latent processes share common components:
- Generation interval: PMF for secondary infection timing
- Initial infections (I0): Starting condition for the renewal process
- Temporal dynamics: How \(\mathcal{R}(t)\) evolves over time
Generation Interval
The generation interval PMF specifies the probability that a secondary infection occurs \(d\) days after the primary infection.
Code
covid_gen_int = [0.16, 0.32, 0.25, 0.14, 0.07, 0.04, 0.02]
gen_int_pmf = jnp.array(covid_gen_int)
gen_int_rv = DeterministicPMF("gen_int", gen_int_pmf)
# Mean generation time
days = np.arange(len(gen_int_pmf))
print(f"Generation interval length: {len(gen_int_pmf)} days")
Generation interval length: 7 days
I0: Initial Infections
The initial infections RV I0_rv specifies the proportion of the
population infected at the first observation time. This must be a
value in the interval (0, 1]. We use a Beta prior centered near a small
value:
Code
I0_rv = DistributionalVariable("I0", dist.Beta(1, 100))
Initial Log Rt
We place a prior on the initial log(Rt), centered at 0.0 (Rt = 1.0) with moderate uncertainty:
Code
initial_log_rt_rv = DistributionalVariable(
"initial_log_rt", dist.Normal(0.0, 0.5)
)
Temporal Processes for \(\mathcal{R}(t)\)
We configure two temporal processes:
- Jurisdiction-level (
baseline_rt_process): AR(1) process for the baseline \(\mathcal{R}(t)\) - Subpopulation-level (
subpop_rt_deviation_process): RandomWalk for subpopulation deviations
The RandomWalk allows flexible evolution of subpopulation-specific transmission without mean reversion.
Code
# AR1 provides mean-reverting behavior for baseline Rt
baseline_rt_process = AR1(autoreg=0.9, innovation_sd=0.05)
# RandomWalk allows flexible subpopulation deviations
subpop_rt_deviation_process = RandomWalk(innovation_sd=0.025)
Observation Processes
Observation processes transform latent infections into observable signals and define the statistical model linking predictions to data. Each observation process:
- Has a unique name that identifies the signal in model outputs
- Declares what infection resolution it needs (
"aggregate"or"subpop") - Applies signal-specific transformations (ascertainment, delay convolution, shedding kinetics)
- Defines the noise model
Signal Naming
Each observation process requires a name parameter—a short, meaningful
identifier like "hospital" or "wastewater". This name serves as the
single identifier for the signal throughout the model:
- Numpyro sites: Prefixes all sample and deterministic sites (e.g.,
hospital_obs,hospital_predicted) - Data binding: Becomes the keyword argument for passing data to
model.run()(e.g.,hospital={...})
This unified naming provides several benefits:
- Interpretable outputs: When examining MCMC samples or posterior
diagnostics, site names like
hospital_predictedimmediately indicate which signal each quantity refers to - Multiple signals of the same type: You can include multiple count observations (e.g., hospital admissions and deaths) by giving each a distinct name
- Clearer debugging: Error messages and trace inspection show meaningful signal names rather than generic identifiers
Hospital Admissions
In this example we use a dataset consisting of hospital admissions for COVID-19 across California for the first 10 months of 2023 (as reported to the CDC).
Code
# Load daily hospital admissions for California
ca_hosp_data = datasets.load_hospital_data_for_state("CA", "2023-11-06.csv")
hosp_admits = ca_hosp_data["daily_admits"]
population_size = ca_hosp_data["population"]
n_hosp_days = ca_hosp_data["n_days"]
print("State: California")
print(f"Population: {population_size:,}")
print(f"Date range: {ca_hosp_data['dates'][0]} to {ca_hosp_data['dates'][-1]}")
print(f"Number of days: {n_hosp_days}")
print(
f"Admissions range: {int(hosp_admits.min())} to {int(hosp_admits.max())}"
)
State: California
Population: 39,512,223
Date range: 2023-01-01 to 2023-11-06
Number of days: 310
Admissions range: 2 to 2574
The hospital admissions data is aggregated at the jurisdiction level,
therefore we specify a Counts observation process.
Code
# Infection-to-hospitalization delay (COVID-19, from literature)
inf_to_hosp_pmf = jnp.array(
[
0,
0.00469,
0.01452,
0.02786,
0.04237,
0.05581,
0.06657,
0.07379,
0.07729,
0.07737,
0.07465,
0.06988,
0.06377,
0.05696,
0.04996,
0.04315,
0.03677,
0.03097,
0.02583,
0.02135,
0.01751,
0.01427,
0.01156,
0.00931,
0.00746,
0.00596,
0.00474,
0.00375,
0.00296,
0.00233,
0.00183,
0.00143,
0.00107,
0.00077,
0.00054,
0.00036,
0.00024,
0.00015,
0.00009,
0.00005,
0.00003,
0.00002,
0.00001,
]
)
hosp_delay_rv = DeterministicPMF("inf_to_hosp_delay", inf_to_hosp_pmf)
# IHR: ~1% of infections lead to hospitalization
ihr_rv = DeterministicVariable("ihr", 0.01)
# Negative binomial concentration (moderate overdispersion)
hosp_concentration_rv = DeterministicVariable("hosp_concentration", 10.0)
# Create hospital observation process
hosp_obs = Counts(
name="hospital",
ascertainment_rate_rv=ihr_rv,
delay_distribution_rv=hosp_delay_rv,
noise=NegativeBinomialNoise(hosp_concentration_rv),
)
print("Hospital observation:")
print(f" Infection resolution: {hosp_obs.infection_resolution()}")
print(f" Delay PMF length: {len(inf_to_hosp_pmf)} days")
Hospital observation:
Infection resolution: aggregate
Delay PMF length: 43 days
Wastewater Concentrations
Wastewater Observation Process
The Measurements base class handles continuous observation processes.
Domain-specific implementations subclass it and implement
_predicted_obs() to transform infections into predicted values. See
observation_processes_measurements.md for a detailed tutorial.
Code
class Wastewater(Measurements):
"""
Wastewater viral concentration observation process.
Transforms site-level infections into predicted log-concentrations
via shedding kinetics convolution and genome/volume scaling.
"""
def __init__(
self,
name: str,
shedding_kinetics_rv: RandomVariable,
log10_genome_per_infection_rv: RandomVariable,
ml_per_person_per_day: float,
noise: MeasurementNoise,
) -> None:
super().__init__(
name=name, temporal_pmf_rv=shedding_kinetics_rv, noise=noise
)
self.log10_genome_per_infection_rv = log10_genome_per_infection_rv
self.ml_per_person_per_day = ml_per_person_per_day
def validate(self) -> None:
shedding_pmf = self.temporal_pmf_rv()
self._validate_pmf(shedding_pmf, "shedding_kinetics_rv")
self.noise.validate()
def lookback_days(self) -> int:
return len(self.temporal_pmf_rv()) - 1
def _predicted_obs(self, infections: ArrayLike) -> ArrayLike:
shedding_pmf = self.temporal_pmf_rv()
log10_genome = self.log10_genome_per_infection_rv()
def convolve_site(site_infections):
convolved, _ = self._convolve_with_alignment(
site_infections, shedding_pmf, p_observed=1.0
)
return convolved
shedding_signal = jax.vmap(convolve_site, in_axes=1, out_axes=1)(
infections
)
genome_copies = 10**log10_genome
concentration = (
shedding_signal * genome_copies / self.ml_per_person_per_day
)
return jnp.log(concentration)
Wastewater Data
For the wastewater data, we use a simulated dataset for California with realistic noise patterns that covers the same time period.
Code
# Load wastewater data for California
ca_ww_data = datasets.load_wastewater_data_for_state("CA", "fake_nwss.csv")
ww_conc = ca_ww_data["observed_conc"] # log concentrations
ww_site_ids = ca_ww_data["site_ids"]
ww_time_indices = ca_ww_data["time_indices"]
ww_n_sites = ca_ww_data["n_sites"]
ww_n_obs = ca_ww_data["n_obs"]
ww_wwtp_names = ca_ww_data["wwtp_names"]
print("State: California")
print(f"Number of sites: {ww_n_sites}")
print(f"Number of observations: {ww_n_obs}")
print(f"Date range: {ca_ww_data['dates'][0]} to {ca_ww_data['dates'][-1]}")
print(
f"Time index range: {int(ww_time_indices.min())} to {int(ww_time_indices.max())}"
)
print("\nSites:")
for i, name in enumerate(ww_wwtp_names[:5]):
print(f" {i}: {name}")
if ww_n_sites > 5:
print(f" ... and {ww_n_sites - 5} more")
State: California
Number of sites: 5
Number of observations: 1495
Date range: 2023-01-01 to 2023-11-06
Time index range: 0 to 309
Sites:
0: 1
1: 2
2: 3
3: 4
4: 5
Wastewater observations are site-level: each measurement is associated with a specific measurement site. The Wastewater observation process uses LogNormalNoise, which takes hierarchical priors for the site-level mode and standard deviation parameters. This enables partial pooling across measurement sites.
Here we specify HierarchicalNormalPrior for the site-level mode and GammaGroupSdPrior for the standard deviation.
Code
# Viral shedding kinetics PMF (days post-infection)
shedding_pmf = jnp.array(
[
0.0,
0.02,
0.08,
0.15,
0.20,
0.18,
0.14,
0.10,
0.06,
0.04,
0.02,
0.01,
]
)
shedding_pmf = shedding_pmf / shedding_pmf.sum() # normalize
shedding_rv = DeterministicPMF("shedding_kinetics", shedding_pmf)
# Log10 genomes shed per infection
log10_genome_rv = DeterministicVariable("log10_genome_per_inf", 9.0)
# Wastewater volume per person per day (mL)
ml_per_person_per_day = 1000.0
# Hierarchical priors for site-level effects
site_mode_prior = HierarchicalNormalPrior(
"ww_site_mode", sd_rv=DeterministicVariable("site_mode_sd", 0.5)
)
site_sd_prior = GammaGroupSdPrior(
"ww_site_sd",
sd_mean_rv=DeterministicVariable("site_sd_mean", 0.3),
sd_concentration_rv=DeterministicVariable("site_sd_conc", 4.0),
)
# Create wastewater observation process
ww_obs = Wastewater(
name="wastewater",
shedding_kinetics_rv=shedding_rv,
log10_genome_per_infection_rv=log10_genome_rv,
ml_per_person_per_day=ml_per_person_per_day,
noise=HierarchicalNormalNoise(site_mode_prior, site_sd_prior),
)
print("Wastewater observation:")
print(f" Infection resolution: {ww_obs.infection_resolution()}")
print(f" Shedding PMF length: {len(shedding_pmf)} days")
Wastewater observation:
Infection resolution: subpop
Shedding PMF length: 12 days
Model Building
We instantiate a PyrenewBuilder object which handles the composition
of the latent infection process and the observation process.
Code
# Build the multi-signal model
builder = PyrenewBuilder()
The PyrenewBuilder object has 3 key methods:
configure_latentadd_observationbuild
Methods configure_latent and add_observation can be called in any
order. Method build is called once all processes have been specified
in the model.
Configuring the Latent Process
We use configure_latent to specify the model structure: generation
interval, initial infections, and temporal dynamics.
Code
print("Latent process configuration:")
print(f" Generation interval length: {len(gen_int_rv())} days")
builder.configure_latent(
HierarchicalInfections,
gen_int_rv=gen_int_rv,
I0_rv=I0_rv,
initial_log_rt_rv=initial_log_rt_rv,
baseline_rt_process=baseline_rt_process,
subpop_rt_deviation_process=subpop_rt_deviation_process,
)
Latent process configuration:
Generation interval length: 7 days
<pyrenew.model.pyrenew_builder.pyrenewbuilder 0x7fdf382bcd70="" at="">
Specifying the Observation Processes, Data
Each observation process’s name attribute becomes the keyword used to
pass that observation’s data to model.run() (e.g., hospital={...},
wastewater={...}).
Code
builder.add_observation(hosp_obs) # Uses hosp_obs.name = "hospital"
builder.add_observation(ww_obs) # Uses ww_obs.name = "wastewater"
model = builder.build()
n_init = model.latent.n_initialization_points
print("Model built successfully")
print(f" n_initialization_points: {n_init}")
print(f" Latent process: {type(model.latent).__name__}")
print(f" Observation processes: {list(model.observations.keys())}")
Model built successfully
n_initialization_points: 42
Latent process: HierarchicalInfections
Observation processes: ['hospital', 'wastewater']
Fitting the Model to Data: model.run()
When you call model.run(), you supply two types of information:
- Observation data — one data dictionary per registered observation process
- Population structure — how the jurisdiction is divided into subpopulations
Shared Time Axis
All observation data uses a shared time axis [0, n_total) where
n_total = n_init + n_days. This shared axis aligns observations with
the internal infection vectors:
- Index 0 corresponds to the first day of the initialization period
- Index
n_initcorresponds to the first day of actual observations - Index
n_total - 1corresponds to the last observation day
The model provides helper methods to align your data with this shared axis:
model.pad_observations(obs)— prependsn_initNaN values to dense observation vectorsmodel.shift_times(times)— addsn_initto sparse time indices
Observation Data by Signal Type
Each observation process’s name attribute becomes the keyword argument
for passing data to model.run():
builder.add_observation(hosp_obs) # hosp_obs.name="hospital" → hospital={...}
builder.add_observation(ww_obs) # ww_obs.name="wastewater" → wastewater={...}
Jurisdiction-level signals (dense)
The jurisdiction-level hospital admissions data is specified as a
Counts observations process with dense data padded to length
n_total:
hospital={
"obs": model.pad_observations(hosp_counts), # shape: (n_total,), NaN-padded
}
The pad_observations method prepends n_init NaN values. NaN marks
the initialization period where predictions exist but observations do
not. You can also use NaN to mark missing data within the observation
period.
Subpopulation-level signals (sparse)
The subpopulation-level wastewater data is specified as a Wastewater
observations process with sparse indexing on the shared time axis:
wastewater={
"obs": jnp.array([...]), # observed log concentrations (n_obs,)
"times": model.shift_times(ww_times), # time indices on shared axis
"subpop_indices": jnp.array([...]), # which subpopulation (selects infection column)
"sensor_indices": jnp.array([...]), # which WWTP/lab pair (selects noise parameters)
"n_sensors": int, # total number of WWTP/lab pairs
}
The shift_times method adds n_init to convert from natural
coordinates (0 = first observation day) to the shared time axis.
Understanding subpop_indices: The latent process generates
infections for all subpopulations as a matrix of shape (T, n_subpops).
Each observation selects which column (subpopulation) it came from using
subpop_indices. This is how observation processes “know” which
subpopulations they observe—the user specifies this mapping at
sample/run time.
A subpopulation is a portion of the jurisdiction’s population (e.g.,
a catchment area). A sensor is a measurement source — typically a
WWTP/lab pair — that produces observations. Multiple sensors can observe
the same subpopulation (e.g., different labs processing samples from the
same catchment), so subpop_indices and sensor_indices may differ.
subpop_indiceslinks each observation to the appropriate infection column (0-indexed into the subpopulations)sensor_indicesselects which sensor’s noise parameters (mode and sd) to apply
Example: A jurisdiction has 6 subpopulations (indices 0-5), where 5
have wastewater monitoring and 1 does not. The subpop_fractions array
has 6 elements. If subpopulation 2 lacks wastewater monitoring,
wastewater observations would have subpop_indices values only in {0,
1, 3, 4, 5}—never 2. The monitored subpopulations need not be
contiguous. The latent process still generates infections for all 6
subpopulations; the wastewater observation just doesn’t see
subpopulation 2.
Population Structure
Population structure is specified via a single array of fractions for all subpopulations:
model.run(
...,
subpop_fractions=jnp.array([...]), # one fraction per subpopulation, must sum to 1
)
This specifies 6 subpopulations with their population fractions. The fractions must sum to 1.0. The latent process generates infections for all 6 subpopulations.
Which subpopulations each observation process “sees” is determined by
the subpop_indices in the observation data, not by the population
structure. For example, if wastewater monitoring covers only 5 of the 6
subpopulations (say, all except subpopulation 2), the wastewater
observation data would have subpop_indices values in {0, 1, 3, 4, 5}
but never 2. The monitored subpopulations can be any subset of {0, …,
n_subpops-1}.
Example model.run() Call
model.run(
num_warmup=500,
num_samples=500,
mcmc_args={"num_chains": 4, "progress_bar": False},
# Model arguments (passed through to sample())
n_days_post_init=n_days,
population_size=population_size,
subpop_fractions=subpop_fractions,
hospital={"obs": model.pad_observations(hosp_counts)},
wastewater={
"obs": ww_conc,
"times": model.shift_times(ww_times),
"subpop_indices": ww_subpop_indices,
"sensor_indices": ww_sensor_indices,
"n_sensors": n_ww_sensors,
},
)
samples = model.mcmc.get_samples()
Running the Model
First we declare the population structure. We have 6 subpopulations, where 5 have wastewater monitoring and 1 does not. The subpopulations with wastewater monitoring need not be contiguous indices—they could be any subset of {0, 1, …, n_subpops-1}.
Code
# All 6 subpopulations with their population fractions
subpop_fractions = jnp.array([0.10, 0.14, 0.21, 0.22, 0.07, 0.26])
n_subpops = len(subpop_fractions)
# Which subpopulations have wastewater monitoring?
# These indices will be used in subpop_indices for wastewater observations.
# They can be any subset of {0, 1, ..., n_subpops-1}, not necessarily contiguous.
ww_monitored_subpops = jnp.array(
[0, 1, 2, 3, 4]
) # subpop 5 has no wastewater monitoring
print(f"Total subpopulations: {n_subpops}")
print(
f"Subpopulations with wastewater monitoring: {list(ww_monitored_subpops)}"
)
print(
f"Wastewater coverage: {float(jnp.sum(subpop_fractions[ww_monitored_subpops])):.0%}"
)
print(f"Total population: {float(jnp.sum(subpop_fractions)):.0%}")
Total subpopulations: 6
Subpopulations with wastewater monitoring: [Array(0, dtype=int64), Array(1, dtype=int64), Array(2, dtype=int64), Array(3, dtype=int64), Array(4, dtype=int64)]
Wastewater coverage: 74%
Total population: 100%
We define a function to prepare observation data using the model’s helper methods to align with the shared time axis.
Code
def prepare_observation_data(
model, n_days_fit, hosp_admits, ww_data, ww_monitored_subpops
):
"""
Prepare observation data for fitting.
Uses model.pad_observations() and model.shift_times() to align data
with the shared time axis.
Parameters
----------
model : MultiSignalModel
The model (provides padding/shifting helpers)
n_days_fit : int
Number of days to include in fit
hosp_admits : array
Hospital admissions time series
ww_data : dict
Wastewater data dictionary
ww_monitored_subpops : array
Indices of subpopulations that have wastewater monitoring.
These are the valid values for subpop_indices in wastewater data.
"""
# Hospital: dense, NaN-padded to length n_total
hosp_obs = model.pad_observations(hosp_admits[:n_days_fit])
# Wastewater: sparse, times shifted to shared axis
ww_mask = ww_data["time_indices"] < n_days_fit
ww_times = model.shift_times(ww_data["time_indices"][ww_mask])
ww_conc = ww_data["observed_conc"][ww_mask]
ww_sensors = ww_data["site_ids"][ww_mask]
# Map wastewater sensors to subpopulation indices
# Each sensor is assigned to one of the monitored subpopulations.
# In practice, this mapping comes from your data (which WWTP serves which catchment).
# For this demo, we cycle sensors through the monitored subpopulations.
n_ww_sensors = ww_data["n_sites"]
n_monitored = len(ww_monitored_subpops)
sensor_to_subpop = {
i: int(ww_monitored_subpops[i % n_monitored])
for i in range(n_ww_sensors)
}
ww_subpop_indices = jnp.array(
[sensor_to_subpop[int(s)] for s in ww_sensors]
)
return {
"hospital": {
"obs": hosp_obs,
},
"wastewater": {
"obs": ww_conc,
"times": ww_times,
"subpop_indices": ww_subpop_indices,
"sensor_indices": ww_sensors,
"n_sensors": n_ww_sensors,
},
}
Fit: 90 Days
Putting this altogether, we align the data with the model time and call
model.run(). We run 4 sampler chains.
Code
# Clear JAX caches to avoid interference from earlier cells
jax.clear_caches()
n_days_90 = 90
obs_data_90 = prepare_observation_data(
model, n_days_90, hosp_admits, ca_ww_data, ww_monitored_subpops
)
print(f"Fitting model with {n_days_90} days of data...")
print(" This may take a few minutes...")
start_time = time.time()
model.run(
num_warmup=500,
num_samples=500,
rng_key=make_rng_key(),
mcmc_args={"num_chains": 4, "progress_bar": False},
n_days_post_init=n_days_90,
population_size=population_size,
subpop_fractions=subpop_fractions,
**obs_data_90,
)
# JAX uses asynchronous dispatch, so we must block until sampling completes
# to get accurate timing
samples_90 = model.mcmc.get_samples()
jax.block_until_ready(samples_90)
elapsed_90 = time.time() - start_time
print(f"Elapsed time: {elapsed_90:.1f} seconds")
Fitting model with 90 days of data...
This may take a few minutes...
Elapsed time: 103.0 seconds
Code
lat_inf_90 = samples_90["latent_infections"]
print(f"Posterior samples shape: {lat_inf_90.shape}")
print(f"Mean latent infections: {np.mean(lat_inf_90):,.0f}")
Posterior samples shape: (2000, 132)
Mean latent infections: 304,939
We check that the chains have converged and the number of effective samples.
Code
# ArviZ diagnostics for 90-day fit
def filter_samples_for_arviz(samples, n_init, num_chains=4):
"""Slice time-series samples to exclude initialization period and reshape for chains."""
num_samples_per_chain = len(list(samples.values())[0]) // num_chains
filtered = {}
for k, v in samples.items():
if v.ndim == 2 and v.shape[1] > n_init:
# Time-series: slice to post-init period, reshape to (chains, draws, time)
filtered[k] = v[:, n_init:].reshape(
num_chains, num_samples_per_chain, -1
)
elif v.ndim == 1:
# Scalar: reshape to (chains, draws)
filtered[k] = v.reshape(num_chains, num_samples_per_chain)
else:
# Multi-dim: reshape to (chains, draws, ...)
filtered[k] = v.reshape(
num_chains, num_samples_per_chain, *v.shape[1:]
)
return filtered
samples_90_filtered = filter_samples_for_arviz(
samples_90, n_init, num_chains=2
)
idata_90 = az.from_dict(posterior=samples_90_filtered)
az.summary(idata_90, var_names=["~latent_infections", "~expected"])
arviz - WARNING - Array contains NaN-value.
| mean | sd | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|---|
| I0 | 0.061 | 0.023 | 0.021 | 0.104 | 0.000 | 0.001 | 2734.0 | 1420.0 | 1.00 |
| hospital_predicted[0] | 1592.540 | 155.672 | 1311.138 | 1887.664 | 3.301 | 2.760 | 2277.0 | 1720.0 | 1.00 |
| hospital_predicted[1] | 1453.297 | 135.442 | 1209.093 | 1714.737 | 2.909 | 2.392 | 2234.0 | 1756.0 | 1.00 |
| hospital_predicted[2] | 1327.815 | 119.350 | 1119.592 | 1568.454 | 2.592 | 2.119 | 2212.0 | 1721.0 | 1.00 |
| hospital_predicted[3] | 1215.977 | 106.654 | 1021.953 | 1416.990 | 2.312 | 1.915 | 2207.0 | 1783.0 | 1.00 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| ww_site_sd_raw[0] | 9.464 | 0.420 | 8.754 | 10.294 | 0.008 | 0.010 | 2615.0 | 1389.0 | 1.00 |
| ww_site_sd_raw[1] | 8.794 | 0.456 | 7.977 | 9.696 | 0.008 | 0.010 | 3364.0 | 1640.0 | 1.00 |
| ww_site_sd_raw[2] | 0.298 | 0.145 | 0.053 | 0.548 | 0.002 | 0.004 | 3300.0 | 1042.0 | 1.00 |
| ww_site_sd_raw[3] | 9.252 | 0.442 | 8.391 | 10.062 | 0.008 | 0.010 | 2906.0 | 1622.0 | 1.00 |
| ww_site_sd_raw[4] | 7.343 | 0.473 | 6.405 | 8.183 | 0.008 | 0.011 | 3674.0 | 1909.0 | 1.01 |
4930 rows × 9 columns
We extract the posterior quantiles and print summary statistics.
Code
def extract_posterior_quantiles(samples, n_init, n_days):
"""Extract posterior quantiles for latent infections."""
latent_inf = np.array(samples["latent_infections"])[
:, n_init : n_init + n_days
]
return {
"q05": np.percentile(latent_inf, 5, axis=0),
"q50": np.percentile(latent_inf, 50, axis=0),
"q95": np.percentile(latent_inf, 95, axis=0),
}
quantiles_90 = extract_posterior_quantiles(samples_90, n_init, n_days_90)
# Summary statistics
ci_width_90 = quantiles_90["q95"] - quantiles_90["q05"]
print(f"Posterior summary for {n_days_90} days:")
print(f" Mean 90% CI width: {ci_width_90.mean():,.0f} infections")
print(f" Median infections (day 45): {quantiles_90['q50'][45]:,.0f}")
Posterior summary for 90 days:
Mean 90% CI width: 95,046 infections
Median infections (day 45): 97,644
Finally, we visualize the posterior latent infections alongside observed hospitalizations. Note that hospital admissions lag behind infections by the infection-to-hospitalization delay (mode ~10 days in our delay PMF). When comparing the two panels, peaks in the infection curve should precede corresponding peaks in hospitalizations by roughly 10-14 days.
Code
# Visualize posterior latent infections and observed hospitalizations (90 days)
# Create separate dataframes for faceted plot
infections_df_90 = pd.DataFrame(
{
"day": np.arange(n_days_90),
"median": quantiles_90["q50"],
"q05": quantiles_90["q05"],
"q95": quantiles_90["q95"],
"signal": "Latent Infections",
}
)
# Add 14-day moving average to smooth noisy daily admissions
hosp_raw_90 = np.array(hosp_admits[:n_days_90], dtype=float)
hosp_ma_90 = (
pd.Series(hosp_raw_90).rolling(window=14, center=True).mean().values
)
hosp_df_90 = pd.DataFrame(
{
"day": np.arange(n_days_90),
"median": hosp_ma_90,
"raw": hosp_raw_90,
"q05": np.nan,
"q95": np.nan,
"signal": "Hospital Admissions (14-day MA)",
}
)
plot_df_90 = pd.concat([infections_df_90, hosp_df_90], ignore_index=True)
plot_df_90["signal"] = pd.Categorical(
plot_df_90["signal"],
categories=["Hospital Admissions (14-day MA)", "Latent Infections"],
ordered=True,
)
(
p9.ggplot(plot_df_90, p9.aes(x="day"))
+ p9.geom_ribbon(
p9.aes(ymin="q05", ymax="q95"),
fill="steelblue",
alpha=0.3,
)
+ p9.geom_point(
p9.aes(y="raw"),
color="gray",
alpha=0.3,
size=1,
)
+ p9.geom_line(
p9.aes(y="median"),
color="darkblue",
size=1,
)
+ p9.facet_wrap("~signal", ncol=1, scales="free_y")
+ p9.scale_y_log10()
+ p9.labs(
x="Day",
y="Count",
title="Posterior Latent Infections vs Observed Hospitalizations (90 days)",
)
+ theme_tutorial
)
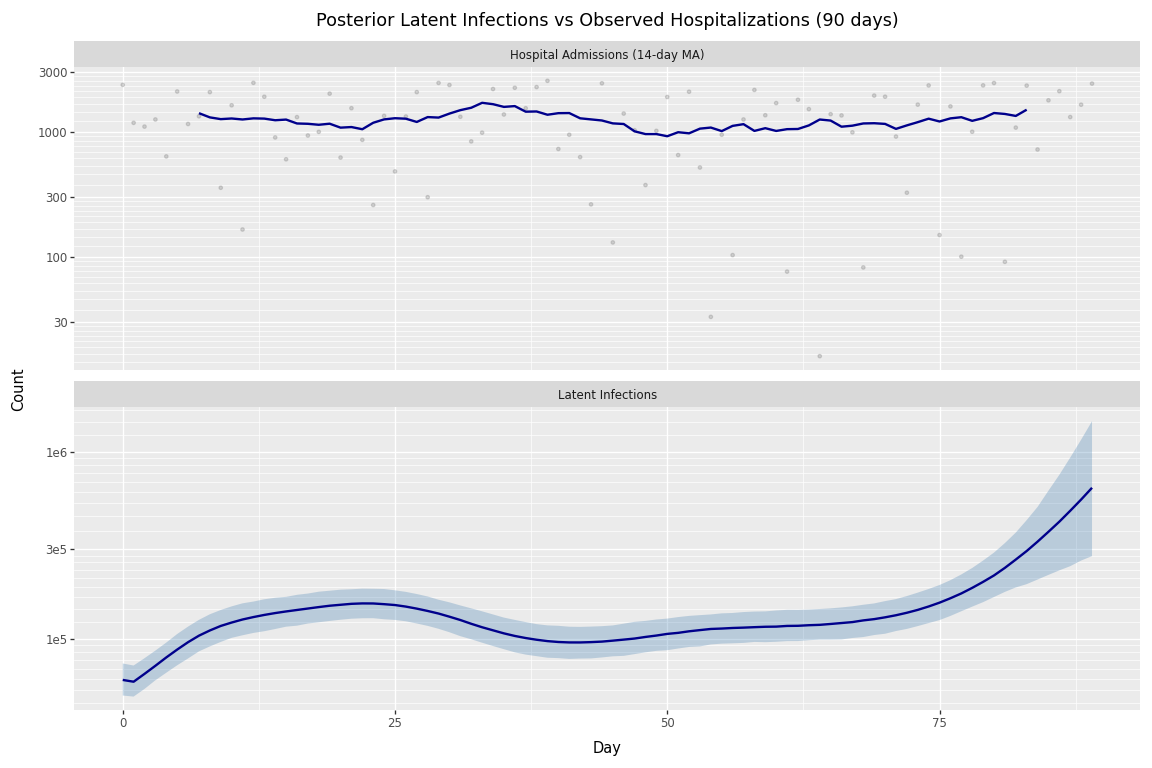
Figure 1: Posterior latent infections and observed hospitalizations (90 days).
Fit: 180 Days
Code
# Clear JAX caches to avoid interference
jax.clear_caches()
n_days_180 = 180
obs_data_180 = prepare_observation_data(
model, n_days_180, hosp_admits, ca_ww_data, ww_monitored_subpops
)
print(f"Fitting model with {n_days_180} days of data...")
print(" This may take a few minutes...")
start_time = time.time()
model.run(
num_warmup=1000,
num_samples=500,
rng_key=make_rng_key(),
mcmc_args={"num_chains": 4, "progress_bar": False},
n_days_post_init=n_days_180,
population_size=population_size,
subpop_fractions=subpop_fractions,
**obs_data_180,
)
# Block until sampling completes for accurate timing
samples_180 = model.mcmc.get_samples()
jax.block_until_ready(samples_180)
elapsed_180 = time.time() - start_time
print(f"Elapsed time: {elapsed_180:.1f} seconds")
Fitting model with 180 days of data...
This may take a few minutes...
Elapsed time: 410.8 seconds
Code
lat_inf_180 = samples_180["latent_infections"]
print(f"Posterior samples shape: {lat_inf_180.shape}")
print(f"Mean latent infections: {np.mean(lat_inf_180):,.0f}")
Posterior samples shape: (2000, 222)
Mean latent infections: 261,502
We check the model fit, as before.
Code
# ArviZ diagnostics for 180-day fit
samples_180_filtered = filter_samples_for_arviz(
samples_180, n_init, num_chains=2
)
idata_180 = az.from_dict(posterior=samples_180_filtered)
az.summary(idata_180, var_names=["~latent_infections", "~expected"])
arviz - WARNING - Array contains NaN-value.
| mean | sd | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|---|
| I0 | 0.098 | 0.028 | 0.049 | 0.152 | 0.001 | 0.001 | 1340.0 | 1492.0 | 1.0 |
| hospital_predicted[0] | 1496.950 | 130.597 | 1258.982 | 1743.714 | 2.716 | 2.313 | 2314.0 | 1584.0 | 1.0 |
| hospital_predicted[1] | 1338.075 | 113.877 | 1137.530 | 1563.670 | 2.375 | 2.064 | 2324.0 | 1531.0 | 1.0 |
| hospital_predicted[2] | 1197.817 | 100.476 | 1013.301 | 1394.132 | 2.119 | 1.842 | 2274.0 | 1425.0 | 1.0 |
| hospital_predicted[3] | 1075.521 | 89.675 | 906.627 | 1247.060 | 1.917 | 1.652 | 2211.0 | 1388.0 | 1.0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| ww_site_sd_raw[0] | 6.996 | 0.312 | 6.406 | 7.560 | 0.007 | 0.006 | 2062.0 | 1642.0 | 1.0 |
| ww_site_sd_raw[1] | 7.161 | 0.335 | 6.545 | 7.822 | 0.006 | 0.007 | 2838.0 | 1606.0 | 1.0 |
| ww_site_sd_raw[2] | 0.304 | 0.153 | 0.063 | 0.607 | 0.003 | 0.004 | 2971.0 | 1107.0 | 1.0 |
| ww_site_sd_raw[3] | 6.582 | 0.291 | 6.050 | 7.134 | 0.006 | 0.006 | 2009.0 | 1688.0 | 1.0 |
| ww_site_sd_raw[4] | 6.504 | 0.427 | 5.735 | 7.338 | 0.008 | 0.011 | 2676.0 | 1354.0 | 1.0 |
8170 rows × 9 columns
Code
quantiles_180 = extract_posterior_quantiles(samples_180, n_init, n_days_180)
ci_width_180 = quantiles_180["q95"] - quantiles_180["q05"]
print(f"Posterior summary for {n_days_180} days:")
print(f" Mean 90% CI width: {ci_width_180.mean():,.0f} infections")
print(f" Median infections (day 90): {quantiles_180['q50'][90]:,.0f}")
Posterior summary for 180 days:
Mean 90% CI width: 55,987 infections
Median infections (day 90): 129,913
Code
# Visualize posterior latent infections and observed hospitalizations (180 days)
infections_df_180 = pd.DataFrame(
{
"day": np.arange(n_days_180),
"median": quantiles_180["q50"],
"q05": quantiles_180["q05"],
"q95": quantiles_180["q95"],
"signal": "Latent Infections",
}
)
# Add 14-day moving average to smooth noisy daily admissions
hosp_raw_180 = np.array(hosp_admits[:n_days_180], dtype=float)
hosp_ma_180 = (
pd.Series(hosp_raw_180).rolling(window=14, center=True).mean().values
)
hosp_df_180 = pd.DataFrame(
{
"day": np.arange(n_days_180),
"median": hosp_ma_180,
"raw": hosp_raw_180,
"q05": np.nan,
"q95": np.nan,
"signal": "Hospital Admissions (14-day MA)",
}
)
plot_df_180 = pd.concat([infections_df_180, hosp_df_180], ignore_index=True)
plot_df_180["signal"] = pd.Categorical(
plot_df_180["signal"],
categories=["Hospital Admissions (14-day MA)", "Latent Infections"],
ordered=True,
)
(
p9.ggplot(plot_df_180, p9.aes(x="day"))
+ p9.geom_ribbon(
p9.aes(ymin="q05", ymax="q95"),
fill="steelblue",
alpha=0.3,
)
+ p9.geom_point(
p9.aes(y="raw"),
color="gray",
alpha=0.3,
size=1,
)
+ p9.geom_line(
p9.aes(y="median"),
color="darkblue",
size=1,
)
+ p9.facet_wrap("~signal", ncol=1, scales="free_y")
+ p9.scale_y_log10()
+ p9.labs(
x="Day",
y="Count",
title="Posterior Latent Infections vs Observed Hospitalizations (180 days)",
)
+ theme_tutorial
)
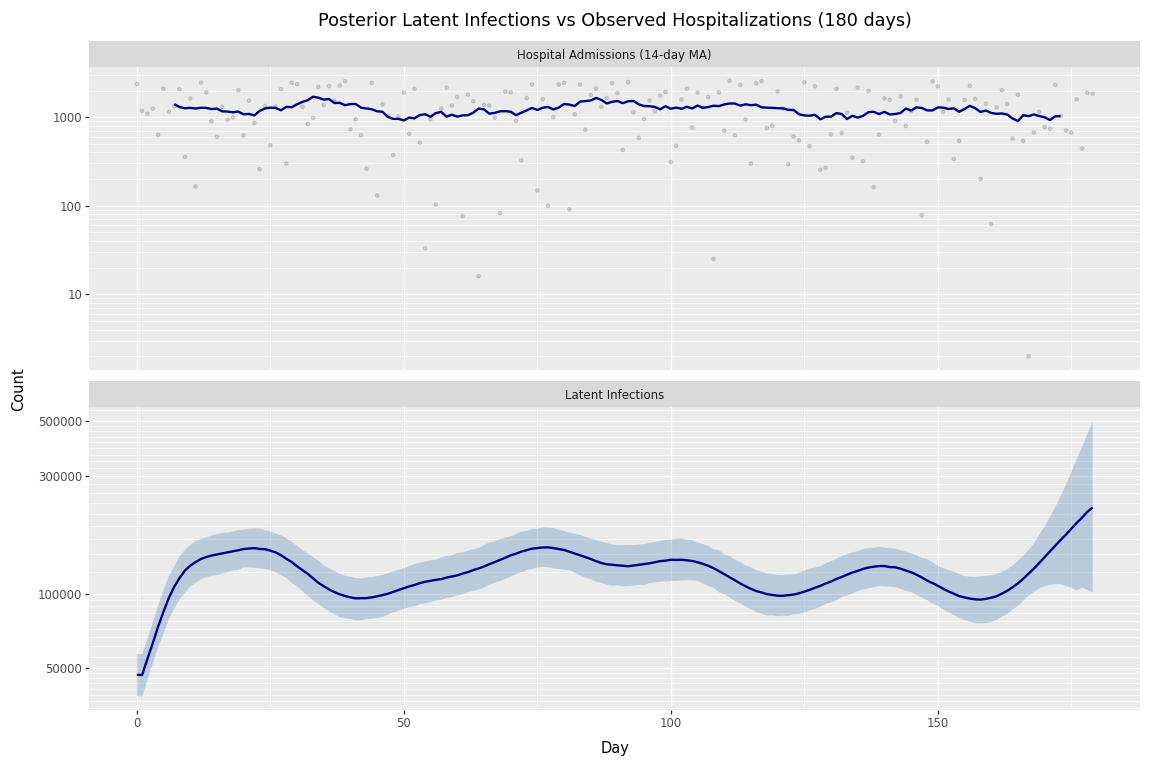
Figure 2: Posterior latent infections and observed hospitalizations (180 days).
Comparing 90-Day vs 180-Day Fits
Comparing the two fits reveals where uncertainty reduction occurs—and why it matters for forecasting.
Code
# Compare CI widths for the overlapping 90-day period
ci_width_90_overlap = quantiles_90["q95"] - quantiles_90["q05"]
ci_width_180_overlap = (
quantiles_180["q95"][:n_days_90] - quantiles_180["q05"][:n_days_90]
)
# Compute difference in CI widths
ci_diff = ci_width_90_overlap - ci_width_180_overlap
ci_ratio = ci_width_90_overlap / ci_width_180_overlap
print("CI Width Comparison (first 90 days):")
print(
f" 90-day fit mean CI width: {ci_width_90_overlap.mean():,.0f} infections"
)
print(
f" 180-day fit mean CI width: {ci_width_180_overlap.mean():,.0f} infections"
)
print(f" Mean difference: {ci_diff.mean():,.0f} infections")
print(f" Mean ratio (90/180): {ci_ratio.mean():.2f}x")
print(
f"\nThe 180-day fit has {(1 - ci_width_180_overlap.mean() / ci_width_90_overlap.mean()) * 100:.1f}% narrower CIs on average"
)
# Per-day comparison
print("\nCI width by time period:")
for start, end, label in [
(0, 30, "Days 0-30"),
(30, 60, "Days 30-60"),
(60, 90, "Days 60-90"),
]:
mean_90 = ci_width_90_overlap[start:end].mean()
mean_180 = ci_width_180_overlap[start:end].mean()
reduction = (1 - mean_180 / mean_90) * 100
print(
f" {label}: 90-day={mean_90:,.0f}, 180-day={mean_180:,.0f}, reduction={reduction:.1f}%"
)
CI Width Comparison (first 90 days):
90-day fit mean CI width: 95,046 infections
180-day fit mean CI width: 47,845 infections
Mean difference: 47,201 infections
Mean ratio (90/180): 1.88x
The 180-day fit has 49.7% narrower CIs on average
CI width by time period:
Days 0-30: 90-day=46,919, 180-day=46,730, reduction=0.4%
Days 30-60: 90-day=42,322, 180-day=42,204, reduction=0.3%
Days 60-90: 90-day=195,896, 180-day=54,601, reduction=72.1%
Notice that the uncertainty reduction is concentrated in days 60-90—the final month of the 90-day window. Earlier periods (days 0-60) show little change because both fits have sufficient future data to constrain those estimates.
This pattern has a direct implication for forecasting: renewal models are most uncertain at the edge of the observation window. Future observations constrain past latent infections through the renewal equation, but when predicting beyond available data, this constraint disappears. The high uncertainty in days 60-90 of the 90-day fit is exactly what we’d expect when forecasting 30 days ahead—there’s no future signal to anchor the estimates.
Summary
This tutorial demonstrated composing a multi-signal renewal model using
PyrenewBuilder:
- Configure latent process (
configure_latent): generation interval, initial infections, temporal dynamics - Add observation processes (
add_observation): each declares its infection resolution and gets a name for data binding - Build and run (
build,model.run): the model routes infections to observations based on resolution and runs NUTS inference
Key Concepts
- Two-part structure: Renewal models separate latent infection dynamics from observation processes
- Infection resolution: Observation processes declare whether they need aggregate or subpop-level infections
- Data routing:
PyrenewBuilderautomatically routes infection trajectories to the appropriate observation processes - Time alignment: Observations must be offset by
n_initialization_pointsto align with model time
Next Steps
- Explore different temporal processes for \(\mathcal{R}(t)\) in the Hierarchical Latent Infections tutorial
- Learn about count-based observation models in Observation Processes: Counts
- Learn about continuous measurement models in Observation Processes: Measurements