Defining Custom PyRenew RandomVariables

This tutorial illustrates how define new RandomVariable classes in order to extend existing models and build new ones, according to PyRenew principles{pyrenew-principles}.

An example of a custom RandomVariable class is the InfectionsWithFeedback class which models the number of infections at time \(t\) as a function of the number of infections at time \(t - \tau\) as follows:

\[I(t) = \mathcal{R}(t) \sum_{\tau = 1}^{T_g} I(t-\tau) g(\tau)\]

where \(\mathcal{R}(t)\) is the reproduction number at time \(t\), and \(g(\tau)\) is the distribution of times from incident infection to secondary infection, i.e., the infectiousness profile.

The reproduction number at time \(t\) is a function of the unadjusted reproduction number at time \(t\) \(\mathcal{R}^\mathrm{u}(t)\) and a damping factor which provides feedback from recent transmission:

\[\mathcal{R}(t) = \mathcal{R}^u(t)\exp\left(-\gamma(t)\sum_{\tau=1}^{T_f}I(t - \tau)f(\tau)\right)\]

where \(\gamma \geq 0\) scales the feedback strength and the function \(f(\tau)\) is the time-scale over which past infections influence the current time-varying reproductive number \(\mathcal{R}(t)\). Because \(\gamma\) is constrained to be positive, this provides a negative feedback mechanism.

import jax
import jax.numpy as jnp
import numpy as np
import numpyro
import numpyro.distributions as dist
from pyrenew.deterministic import DeterministicPMF, DeterministicVariable
from pyrenew.latent import InfectionsWithFeedback
from pyrenew.model import RtInfectionsRenewalModel
from pyrenew.process import RandomWalk
from pyrenew.metaclass import RandomVariable
from pyrenew.randomvariable import DistributionalVariable, TransformedVariable
from pyrenew.latent import (
    InfectionInitializationProcess,
    InitializeInfectionsExponentialGrowth,
)
import pyrenew.transformation as t

/home/runner/work/PyRenew/PyRenew/.venv/lib/python3.13/site-packages/tqdm/auto.py:21: TqdmWarning: IProgress not found. Please update jupyter and ipywidgets. See https://ipywidgets.readthedocs.io/en/stable/user_install.html
  from .autonotebook import tqdm as notebook_tqdm

Expected Behavior of the Feedback Mechanism

This section demonstrates how to use the InfectionsWithFeedback class to model the number of infections by running a baseline simulation. We simulate the model without an observation process which lets us see how the feedback mechanism affects the reproduction number and subsequent infections over time.

The following code-chunks define the model components in the following order.

We define a deterministic PMF gen_int_array, the discretized fraction of infectiousness per day. For this example, we have a 4-day PMF of equal probabilities with feedback strength (\(\gamma\)) set to 0.01 to create moderate damping.
We specify the InfectionInitializationProcess class, where the number of latent infections immediately before the renewal process begins follows a log-normal distribution with mean = 0 and standard deviation = 1.
We specify the InfectionsWithFeedback component using the same distribution as the generation interval.
The latent random variable \(\mathcal{R}^\mathrm{u}(t)\) is estimated via random walk on \(\log(\mathcal{R}^\mathrm{u}(t))\), (as in the basic renewal model).

gen_int_array = jnp.array([0.25, 0.25, 0.25, 0.25])
gen_int = DeterministicPMF(name="gen_int", value=gen_int_array)
feedback_strength = DeterministicVariable(name="feedback_strength", value=0.01)

# | label: model-components
I0 = InfectionInitializationProcess(
    "I0_initialization",
    DistributionalVariable(name="I0", distribution=dist.LogNormal(0, 1)),
    InitializeInfectionsExponentialGrowth(
        gen_int_array.size,
        DeterministicVariable(name="rate", value=0.05),
    ),
)

latent_infections = InfectionsWithFeedback(
    infection_feedback_strength=feedback_strength,
    infection_feedback_pmf=gen_int,
)


class MyRt(RandomVariable):
    def validate(self):
        pass

    def sample(self, n: int, **kwargs) -> tuple:
        sd_rt = numpyro.sample("Rt_random_walk_sd", dist.HalfNormal(0.025))

        rt_rv = TransformedVariable(
            name="log_rt_random_walk",
            base_rv=RandomWalk(
                name="log_rt",
                step_rv=DistributionalVariable(
                    name="rw_step_rv", distribution=dist.Normal(0, sd_rt)
                ),
            ),
            transforms=t.ExpTransform(),
        )
        rt_init_rv = DistributionalVariable(
            name="init_log_rt", distribution=dist.Normal(0, 0.2)
        )
        init_rt = rt_init_rv.sample()

        return rt_rv.sample(n=n, init_vals=init_rt, **kwargs)

We build the model from these components and then simulate data from it without observed infections.

model0 = RtInfectionsRenewalModel(
    gen_int_rv=gen_int,
    I0_rv=I0,
    latent_infections_rv=latent_infections,
    Rt_process_rv=MyRt(),
    infection_obs_process_rv=None,  # no observed infections
)

# Sampling and fitting model 0 (with no obs for infections)
with numpyro.handlers.seed(rng_seed=223):
    model0_samp = model0.sample(n_datapoints=30)

import matplotlib.pyplot as plt

fig, ax = plt.subplots()
ax.plot(model0_samp.latent_infections)
ax.set_xlabel("Time")
ax.set_ylabel("Infections")
plt.show()

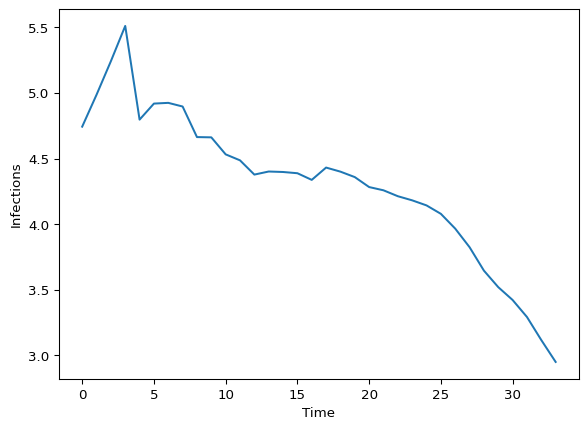
Figure 1: Simulated infections with no observation process

With feedback strength \(\gamma = 0.01\), we see:

Initial exponential-like growth when infection history is minimal
Damping effects becoming visible as infections accumulate

PyRenew’s `RandomVariable` class

Fundamentals

All instances of PyRenew’s RandomVariable should have at least three functions: __init__(), validate(), and sample(). The __init__() function is the constructor and initializes the class. The validate() function checks if the class is correctly initialized. Finally, the sample() method contains the core of the class; it should return a tuple or namedtuple. The following is a minimal example of a RandomVariable class based on numpyro.distributions.Normal:

from pyrenew.metaclass import RandomVariable


class MyNormal(RandomVariable):
    def __init__(self, loc, scale):
        self.validate(scale)
        self.loc = loc
        self.scale = scale
        return None

    @staticmethod
    def validate(self):
        if self.scale <= 0:
            raise ValueError("Scale must be positive")
        return None

    def sample(self, **kwargs):
        return (dist.Normal(loc=self.loc, scale=self.scale),)

The @staticmethod decorator exposes the validate function to be used outside the class.

Essential elements of class `InfectionsWithFeedback`

As an exercise we define a new class InfFeedback, which exactly follows the InfectionsWithFeedback class, but omits the tedious checks on its inputs.

Although returning a namedtuple is not strictly required, they are the recommended return type, as they make the code more readable. The following code-chunk shows how to create a namedtuple for the InfectionsWithFeedback class:

from collections import namedtuple

# Creating a tuple to store the output
InfFeedbackSample = namedtuple(
    typename="InfFeedbackSample",
    field_names=["post_initialization_infections", "rt"],
    defaults=(None, None),
)

The next step is to create the actual class. The bulk of its implementation lies in the function pyrenew.latent.compute_infections_from_rt_with_feedback(). We will also use the pyrenew.arrayutils.pad_edges_to_match() function to ensure the passed vectors match their lengths. The following code-chunk shows most of the implementation of the InfectionsWithFeedback class:

# Creating the class
from pyrenew.metaclass import RandomVariable
from pyrenew.latent import compute_infections_from_rt_with_feedback
from pyrenew import arrayutils as au
from jax.typing import ArrayLike
import jax.numpy as jnp


class InfFeedback(RandomVariable):
    """Latent infections"""

    def __init__(
        self,
        infection_feedback_strength: RandomVariable,
        infection_feedback_pmf: RandomVariable,
    ) -> None:
        """Constructor"""

        self.infection_feedback_strength = infection_feedback_strength
        self.infection_feedback_pmf = infection_feedback_pmf

        return None

    def validate(self):
        """
        Generally, this method should be more meaningful, but we will skip it for now
        """
        return None

    def sample(
        self,
        Rt: ArrayLike,
        I0: ArrayLike,
        gen_int: ArrayLike,
        **kwargs,
    ) -> tuple:
        """Sample infections with feedback"""

        # Generation interval
        gen_int_rev = jnp.flip(gen_int)

        # Baseline infections
        I0_vec = I0[-gen_int_rev.size :]

        # Sampling inf feedback strength and adjusting the shape
        inf_feedback_strength = self.infection_feedback_strength(
            **kwargs,
        )

        inf_feedback_strength = jnp.atleast_1d(inf_feedback_strength)

        inf_feedback_strength, _ = au.pad_edges_to_match(
            x=inf_feedback_strength,
            y=Rt,
        )

        # Sampling inf feedback and adjusting the shape
        inf_feedback_pmf = self.infection_feedback_pmf(**kwargs)
        inf_fb_pmf_rev = jnp.flip(inf_feedback_pmf)

        # Generating the infections with feedback
        all_infections, Rt_adj = compute_infections_from_rt_with_feedback(
            I0=I0_vec,
            Rt_raw=Rt,
            infection_feedback_strength=inf_feedback_strength,
            reversed_generation_interval_pmf=gen_int_rev,
            reversed_infection_feedback_pmf=inf_fb_pmf_rev,
        )

        # Storing adjusted Rt for future use
        numpyro.deterministic("Rt_adjusted", Rt_adj)

        # Preparing the output

        return InfFeedbackSample(
            post_initialization_infections=all_infections,
            rt=Rt_adj,
        )

The core of the class is implemented in the sample() method. Things to highlight from the above code:

Arguments of sample: The InfFeedback class will be used within RtInfectionsRenewalModel to generate latent infections. During the sampling process, InfFeedback() will receive the reproduction number, the initial number of infections, and the generation interval. RandomVariable() calls are expected to include the **kwargs argument, even if unused.
Saving computed quantities: Since Rt_adj is not generated via numpyro.sample(), we use numpyro.deterministic() to record the quantity to a site; allowing us to access it later.
Return type of InfFeedback(): As said before, the sample() method should return a tuple or namedtuple. In our case, we return a namedtuple InfFeedbackSample with two fields: infections and rt.

To check our work, we build a second model using our new class InfFeedback and compare it to our first model, which uses the built-in InfectionsWithFeedback class. Since class InfFeedback exactly follows the InfectionsWithFeedback class, if correctly implemented, the two models should provide exactly the same predictions.

latent_infections2 = InfFeedback(
    infection_feedback_strength=feedback_strength,
    infection_feedback_pmf=gen_int,
)

model1 = RtInfectionsRenewalModel(
    gen_int_rv=gen_int,
    I0_rv=I0,
    latent_infections_rv=latent_infections2,
    Rt_process_rv=MyRt(),
    infection_obs_process_rv=None,
)

# Sampling and fitting model 0 (with no obs for infections)
with numpyro.handlers.seed(rng_seed=223):
    model1_samp = model1.sample(n_datapoints=30)

Comparing model0 with model1, these two should match:

import matplotlib.pyplot as plt

fig, ax = plt.subplots(ncols=2)
ax[0].plot(model0_samp.latent_infections)
ax[1].plot(model1_samp.latent_infections)
ax[0].set_xlabel("Time (model 0)")
ax[1].set_xlabel("Time (model 1)")
ax[0].set_ylabel("Infections")
plt.show()

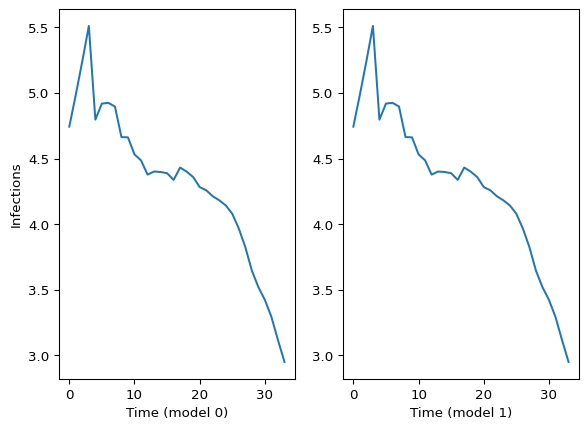
Figure 2: Comparing latent infections from model 0 and model 1

Defining Custom PyRenew RandomVariables

Expected Behavior of the Feedback Mechanism

PyRenew’s RandomVariable class

Fundamentals

Essential elements of class InfectionsWithFeedback

PyRenew’s `RandomVariable` class

Essential elements of class `InfectionsWithFeedback`